(本题满分16分;第(1)小题5分,第(2)小题5分,第三小题6分)
已知函数 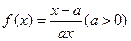
(1)判断并证明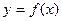 在
在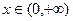 上的单调性;
上的单调性;
(2)若存在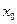 ,使
,使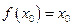 ,则称
,则称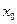 为函数
为函数 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求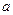 的值;
的值;
(3)若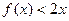 在
在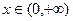 上恒成立 , 求
上恒成立 , 求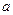 的取值范围.
的取值范围.
(本题满分16分,第一小题8分;第二小题8分)
已知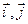 是
是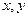 轴正方向的单位向量,设
轴正方向的单位向量,设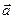 =
=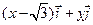 ,
, 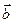 =
= ,且满足
,且满足 .
.
(1)求点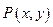 的轨迹方程;
的轨迹方程;
(2) 过点 的直线
的直线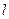 交上述轨迹于
交上述轨迹于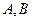 两点,且
两点,且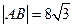 ,求直线
,求直线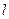 的方程.
的方程.
(本小题满分16分)已知函数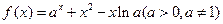 .
.
(Ⅰ)当 时,求证:函数
时,求证:函数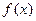 在
在 上单调递增;
上单调递增;
(Ⅱ)若函数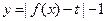 有三个零点,求
有三个零点,求 的值;
的值;
(Ⅲ)若存在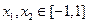 ,使得
,使得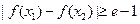 ,试求
,试求 的取值范围.
的取值范围.
(本小题满分16分)已知数列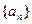 是以
是以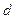 为公差的等差数列,数列
为公差的等差数列,数列 是以
是以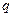 为公比的等比数列.
为公比的等比数列.
(Ⅰ)若数列 的前
的前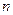 项和为
项和为 ,且
,且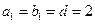 ,
, ,求整数
,求整数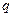 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列 中是否存在一项
中是否存在一项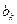 ,使得
,使得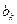 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续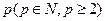 项的和?请说明理由;
项的和?请说明理由;
(Ⅲ)若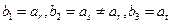 (其中
(其中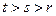 ,且(
,且(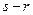 )是(
)是(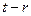 )的约数),
)的约数),
求证:数列 中每一项都是数列
中每一项都是数列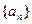 中的项.
中的项.
(本小题满分16分)已知⊙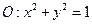 和点
和点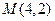 .
.
(Ⅰ)过点 向⊙
向⊙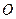 引切线
引切线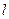 ,求直线
,求直线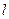 的方程;
的方程;
(Ⅱ)求以点 为圆心,且被直线
为圆心,且被直线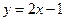 截得的弦长4的⊙
截得的弦长4的⊙ 的方程;
的方程;
(Ⅲ)设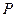 为(Ⅱ)中⊙
为(Ⅱ)中⊙ 上任一点,过点
上任一点,过点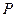 向⊙
向⊙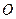 引切线,切点为Q. 试探究:平面内是否存在一定点
引切线,切点为Q. 试探究:平面内是否存在一定点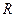 ,使得
,使得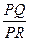 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
已知点(1, )是函数
)是函数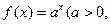 且
且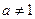 )的图象上一点,等比数列
)的图象上一点,等比数列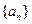 的前
的前 项和为
项和为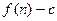 ,数列
,数列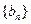
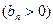 的首项为
的首项为 ,且前
,且前 项和
项和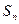 满足
满足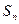 -
-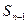 =
=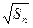 +
+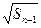 (
(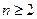 ).
).
(1)求数列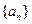 和
和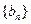 的通项公式;
的通项公式;
(2)若数列{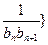 前
前 项和为
项和为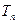 ,问
,问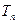 >
>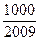 的最小正整数
的最小正整数 是多少? .
是多少? . 

已知圆C:x2+y2+2x-4y+3=0;
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程。
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标。
(本题18分)
已知:正数数列 的通项公式
的通项公式
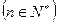
(1)求数列 的最大项;
的最大项;
(2)设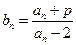 ,确定实常数
,确定实常数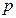 ,使得
,使得 为等比数列;
为等比数列;
(3)(理)数列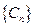 ,满足
,满足 ,
, ,其中
,其中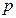 为第(2)小题中确定的正常数,求证:对任意
为第(2)小题中确定的正常数,求证:对任意 ,有
,有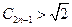 且
且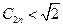 或
或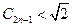 且
且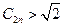 成立.
成立.
(文)设 是满足第(2)小题的等比数列,求使不等式
是满足第(2)小题的等比数列,求使不等式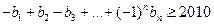 成立的最小正整数
成立的最小正整数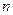 .
.
(本题16分)
如图,F是抛物线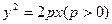 的焦点,Q是准线与
的焦点,Q是准线与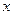 轴的交点,斜率为
轴的交点,斜率为 的直线
的直线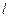 经过点Q.
经过点Q.
(1)当K取不同数值时,求直线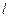 与抛物线交点的个数;
与抛物线交点的个数;
(2)如直线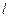 与抛物线相交于A、B两点,求证:
与抛物线相交于A、B两点,求证: 是定值
是定值
(3)在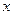 轴上是否存在这样的定点M,对任意的过点Q的直线
轴上是否存在这样的定点M,对任意的过点Q的直线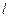 ,如
,如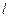 与抛物线相交于A、B两点,均能使得
与抛物线相交于A、B两点,均能使得 为定值,有则找出满足条
为定值,有则找出满足条
件的点M;没有,则说明理由.
(本题16分)
如图所示,某人在斜坡P处仰视正对 面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为
面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为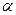 ,
,
(1)以射线OC为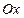 轴的正向,OB为
轴的正向,OB为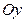 轴正向,建立直角坐标系,求
轴正向,建立直角坐标系,求 出斜坡CD所在直线方程;
出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).
(本题14分)
△ABC中,角A、B、C的对边依次为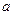 、
、 、
、 .已知
.已知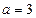 ,
,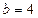 ,外接圆半径
,外接圆半径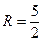 ,
, 边长为整数,
边长为整数,
(1)求∠A的大小(用反三角函数表示);
(2)求边长 ;
;
(3)在AB、AC上分别有点D、E,线段DE将△ABC分成面积相等的两部分,求线段DE长的最小值.
(本题14分)
如图,四棱锥 中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD
中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD 的中点
的中点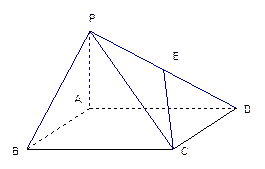
(1)求异面直线PA与CE所成角的大小;
(2)(理)求二面角E-AC-D的大小。
(文)求三棱锥A-CDE的体积。
试题篮
()