高中数学解答题

（本小题满分12分）
如图，在四棱锥S—ABCD中，底面ABCD为矩形，SA⊥平面ABCD，二面角S—
CD—A的平面角为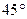，M为AB中点，N为SC中点.
（1）证明：MN//平面SAD；
（2）证明：平面SMC⊥平面SCD；

  （3）若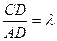，求实数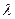的值，使得直线SM与平面SCD所成角为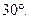

 

（本小题满分12分）
设O为坐标原点，点P的坐标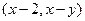
（I）在一个盒子中，放有标号为1，2，3的三张卡片，现从此盒中有放回地先后抽到两张卡片的标号分别记为x，y，求|OP|的最大值，并求事件“|OP|取到最大值”的概率；
（II）若利用计算机随机在[0，3]上先后取两个数分别记为x，y，求P点在第一象限的概率.

（本小题满分12分）
在
（1）求角C的大小；
（2）若AB边的长为，求BC边的长.

（本小题满分12分）
已知函数
（1）确定上的单调性；
（2）设在（0，2）上有极值，求的取值范围。

（本小题满分12分）
已知半圆，动圆与此半圆相切且与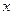轴相切。
（1）求动圆圆心的轨迹，并画出其轨迹图形；
（2）是否存在斜率为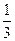的直线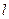，它与（1）中所得轨迹的曲线由左到右顺次交于A、B、C、D四点，且满足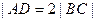。若存在，求出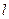的方程；若不存在，说明理由。

在△ABC中，的垂直平分线分别交AB，AC于E，E（图一），沿DE将△ADE折起，使得平面ADE⊥平面BDEC（图二）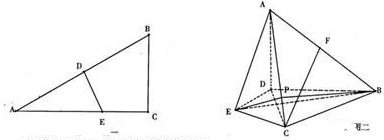

（1）若F是AB的中点，求证：平面ACD⊥平面ADE
（2）P是AC上任意一点，求证：平面ACD⊥平面PBE
（3）P是AC上一点，且AC⊥平面PBE，求二面角P-BE-C的大小

（本小题满分12分）
在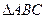中，角A、B、C所对的边分别为，且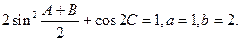
（1）求C和；
（2）P为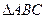内任一点（含边界），点P到三边距离之和为，设P到AB，BC距离分别为，用表示并求的取值范围。

（本小题满分12分）
甲、乙、丙三台机床各自独立的加工同一种零件，已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8，乙、丙两台机床加工的零件数相等，甲机床加工的零件数是乙机床加工的零件的二倍。
（1）从甲、乙、丙加工的零件中各取一件检验，示至少有一件一等品的概率；
（2）将三台机床加工的零件混合到一起，从中任意的抽取一件检验，求它是一等品的概率；
（3）将三台机床加工的零件混合到一起，从中任意的抽取4件检验，其中一等品的个数记为X，求EX。

（本小题满分14分）
已知：有穷数列{a_n}共有2k项（整数k≥2 ）,a₁="2" ,设该数列的前n项和为 S_n且满足S_n+1=aS_n+2（n=1,2,…,2k-1）,a＞1．
（1）求{a_n}的通项公式;
（2）设b_n=log₂a_n，求{b_n}的前n项和T_n;
（3）设c_n=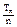，若a=2，求满足不等式 + +…++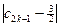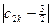≥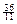时k的最小值．

（本小题满分12分）
已知函数f（x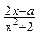）=（x∈R）．
⑴当f（1）=1时，求函数f（x）的单调区间；
⑵设关于x的方程f（x）=的两个实根为x₁,x₂，且-1≤a≤1,求｜x₁-x₂｜的最大值；
⑶在（2）的条件下，若对于［-1，1］上的任意实数t，不等式m²+tm+1≥｜x₁-x₂｜恒成立，求实数m的取值范围．

（本小题满分12分）
从某校高三年级800名男生中随机抽取50名学生测量其身高，据测量被测学生的身高全部在155cm到195cm之间．将测量结果按如下方式分成8组：第一组［155，160），第二组［160，165），……，第八组［190，195］，如下图是按上述分组得到的频率分布直方图的一部分．已知：第1组与第8组的人数相同，第6组、第7组和第8组的人数依次成等差数列．
⑴求下列频率分布表中所标字母的值，并补充完成频率分布直方图；

分组	频数	频率	频率/组距
…	…	…	…
[180，185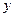）			z
[185，190）	m	n	p
…	…	…	…

⑵若从身高属于第6组和第8组的所有男生中随机的抽取2名男生，记他们的身高分别为x、y，求满足：｜x-y｜≤ 5事件的概率．

（本小题满分12分）
已知椭圆C: +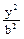=1（a＞b＞0）的离心率e=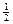，且椭圆经过点N（2，-3）．
（1）求椭圆C的方程；
（2）求椭圆以M（-1，2）为中点的弦所在直线的方程．

（本小题满分12分）
如图，棱柱ABCD-A₁B₁C₁D₁的底面ABCD为菱形，平面AA₁C₁C⊥平面ABC  D．
（1）证明：BD⊥AA₁；
（2）证明：平面AB₁C//平面DA₁C₁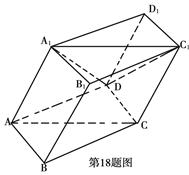
    （3）在直线CC₁上是否存在点P，使BP//平面DA₁C₁？若存在，求出点P的位置；若不存在，说明理由．

（本小题满分12分）
已知：在△ABC中，a,b,c分别是角A、B、C所对的边，向量m=（2sin，），
n=（sin+，1）且m·n=．
（1）求角B的大小;
（2）若角B为锐角，a=6,S_△ABC=6,求b的值．