设O为坐标原点,动点M在椭圆
上,过M做x轴的垂线,垂足为N,点P满足
.
(1) 求点 P的轨迹方程;
(2) 设点 Q在直线 上,且 .证明:过点 P且垂直于 的直线 l过 C的左焦点 F.
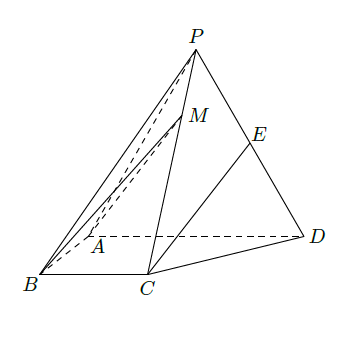
如图,四棱锥
中,侧面
为等比三角形且垂直于底面
,
是
的中点.
(1)证明:直线 平面 ;
(2)点 M在棱 PC上,且直线 BM与底面 ABCD所成锐角为 ,求二面角 的余弦值.
淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg)某频率直方图如下:
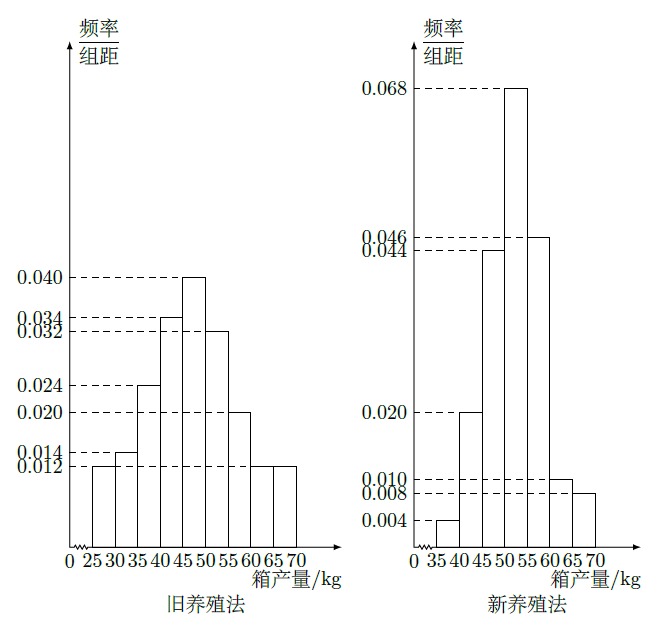
(1)设两种养殖方法的箱产量相互独立,记A表示事件:旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg |
箱产量≥50kg |
|
旧养殖法 |
||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01)
P( |
0.050 |
0.010 |
0.001 |
k |
3.841 |
6.635 |
10.828 |
一批产品的二等品率为
,从这批产品中每次随机取一件,有放回地抽取
次,
表示抽到的二等品件数,则
.
已知
是边长为2的等边三角形,P为平面ABC内一点,则
的最小值是( )
A.. . B. C. D.
已知直三棱柱
中,
,
,
,则异面直线
与
所成角的余弦值为( )
A. B. C. D.
若双曲线  (
,
)的一条渐近线被圆
所截得的弦长为2,则
的离心率为( )
(
,
)的一条渐近线被圆
所截得的弦长为2,则
的离心率为( )
A.2 B. C. D.
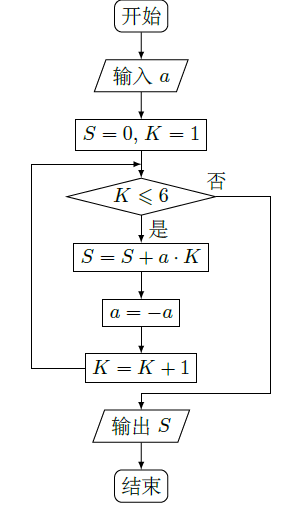
执行右面的程序框图,如果输入的
,则输出的
( )
| A. | 2 |
B. | 3 |
C. | 4 |
D. | 5 |
试题篮
()