高中物理相互作用、力与机械试题

小明用如图所示装置来“探究求合力的方法”，图中弹簧秤B的读数为      N．若顺时针转动弹簧秤B，同时保持结点O的位置和弹簧秤A的拉力方向不变，此过程两弹簧秤间的夹角α始终大于90°且示数均不超出量程，则弹簧秤A的示数      （选填“增大”、“减小”或“不变”），弹簧秤B的示数      （选填“增大”、“减小”或“不变”）．

如图所示，质量为m₁=5kg的滑块置于一粗糙的斜面上，用一平行于斜面的大小为30N的力F推滑块，滑块沿斜面向上匀速运动，斜面体质量m₂=10kg，且始终静止，取g=10m/s²，求：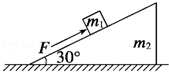

（1）斜面对滑块的摩擦力．
（2）地面对斜面体的摩擦力和支持力．

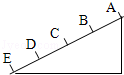
如图所示，光滑斜面AE被分成四个相等的部分，一物体由A点从静止释放，下列结论中正确的是（ ）

A．物体到达各点的速率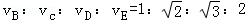

B．物体到达各点所经历的时间：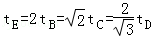

C．物体从A到E的平均速度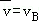

D．物体通过每一部分时，其速度增量vB﹣vA=vC﹣vB=vD﹣vC=vE﹣vD

如图所示，质量为M的三角形木块a，放在水平面上，把另一质量为m的木块b放在a的斜面上，斜面的倾角为θ，对a施一水平力F，使b不沿斜面滑动，不计一切摩擦，则b对a的压力为（ ）

A．

B．mgcosθ

C．

D．

三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同，它们共同悬挂一重物，如图所示，其中OB是水平的，A端、B端固定．若逐渐增加C端所挂物体的质量，则最先断的绳（ ）

A．必定是OA    B．必定是OB
C．必定是OC    D．可能是OB，也可能是OC

如图，一不可伸长的轻质细绳跨过滑轮后，两端分别悬挂质量为m₁和m₂的物体A和B．若滑轮转动时与绳滑轮有一定大小，质量为m且分布均匀，滑轮转动时与绳之间无相对滑动，不计滑轮与轴之间的摩擦．设细绳对A和B的拉力大小分别为T₁和T₂，已知下列四个关于T₁的表达式中有一个是正确的，请你根据所学的物理知识，通过一定的分析判断正确的表达式是（ ）

A．T₁=    B．T₁=
C．T₁=    D．T₁=

如图，一不可伸长的光滑轻绳，其左端固定于O点，右端跨过位于O′点的固定光滑轴悬挂一质量为M的物体；OO′段水平，长度为L；绳子上套一可沿绳滑动的轻环．现在轻环上悬挂一钩码，平衡后，物体上升L．则钩码的质量为（ ）

A．M

B．M

C．M

D．M

如图所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角．若在B点悬挂一个定滑轮（不计重力），某人用它匀速地提起重物．已知重物的质量m=30kg，人的质量M=50kg，g取10m/s²．试求：

（1）此时地面对人的支持力的大小；
（2）轻杆BC和绳AB所受力的大小．

如图所示，在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体A，A的左端紧靠竖直墙，A与竖直墙之间放一光滑圆球B，整个装置处于静止状态，若把A向右移动少许后，它们仍处于静止状态，则（ ）

A．球B对墙的压力减小

B．物体A与球B之间的作用力增大

C．地面对物体A的摩擦力减小

D．物体A对地面的压力减小

如图所示，固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔，质量为m的小球套在圆环上，一根细线的下端系着小球，上端穿过小孔用力F拉住，绳与竖直方向夹角为θ，小球处于静止状态．设小球受支持力为F_N，则下列关系正确的是（ ）

A．F=2mgcosθ

B．F=mgcosθ

C．FN=2mg

D．FN=mg

如图所示，轻弹簧两端拴接两个质量均为m的小球a、b，拴接小球的细线固定在天花板上，两球静止，两细线与水平方向的夹角均为α=30⁰，弹簧水平，以下说法正确的是（      ）

A．细线的拉力大小为2mg

B．弹簧的弹力大小为mg

C．剪断左侧细线瞬间，b球加速度大小为g

D．剪断弹簧最右侧瞬间，a球加速度大小为0

如图所示，开口向下的“┍┑”形框架，两侧竖直杆光滑固定，上面水平横杆中点固定一定滑轮，两侧杆上套着的两滑块用轻绳绕过定滑轮相连，并处于静止状态，此时连接滑块A的绳与水平方向夹角为θ，连接滑块B的绳与水平方向的夹角为2θ，则A、B两滑块的质量之比为（    ）

A．2sinθ：1   B．2cosθ：1   C．1：2cosθ   D．1：2sinθ

如图所示，质量均为m的小球A、B用两根不可伸长的轻绳连接后悬挂于O点，在外力F的作用下，小球A、B处于静止状态．若要使两小球处于静止状态且悬线OA与竖直方向的夹角θ保持30°不变，则外力F的大小可能为（ ）

A.   B.mg  C. 2mg  D．100mg

如图所示，在粗糙的水平地面上有一个质量为1Kg的木箱，在一个跟水平面成θ=37°角的斜向下的恒力F作用下，木箱恰能向右匀速滑行，已知木箱与地面间的动摩擦因素为0.5，求恒力F的大小。
 

两个共点力的合力最大值为25N，最小值为15N，则这两个力分别为____ N、____N。