如图所示，将底部装有弹簧的木箱在某一高度由静止释放，从弹簧接触地面到木箱速度为零的过程中，木箱速度的变化情况是
| A．一直增大 | B．一直减小 | C．先减小后增大 | D．先增大后减小 |
伽利略相信，自然界的规律是简洁明了的．他从这个信念出发，认为落体一定是最简单的变速运动，并研究得出落体的速度
| A．与落体质量成正比 | B．与落体体积成正比 |
| C．与下落高度成正比 | D．与运动时间成正比 |
甲物体的重量比乙物体大5倍，甲从H高处自由落下，乙从2H高处与甲物体同时自由落下，忽略空气阻力，在它们落地之前，下列说法中正确的是（ ）
| A．两物体下落过程中，在同一时刻甲的速度比乙的速度大 |
B．各自下落 时，它们的速度相同 |
| C．下落过程中甲的加速度比乙的加速度大 |
| D．甲乙经过同一高度处，它们的速度相同 |
伽利略对自由落体的研究，开创了研究自然规律的科学方法，这就是（ ）
| A．对自然现象进行总结归纳的方法 |
| B．用科学实验进行探究的方法 |
| C．对自然现象进行总结归纳，并用实验进行验证的方法 |
| D．抽象思维、数学推导和科学实验相结合的方法 |
伽利略对自由落体运动的研究，是科学实验和逻辑思维的完美结合，如图所示，可大致表示其实验和思维的过程，对这一过程的分析，下列说法正确的是（ ）
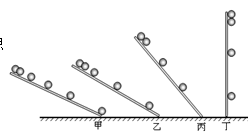
| A．其中的甲、乙、丙图是实验现象，丁图是经过合理的外推得到的结论 |
| B．其中的丁图是实验现象，甲、乙、丙图是经过合理的外推得到的结论 |
| C．运用丁图的实验，可“放大”重力的作用，使实验现象更明显 |
| D．运用甲图的实验，可“冲淡”重力的作用，使实验现象更明显 |
如图所示，质量为
的半圆轨道小车静止在光滑的水平地面上，其水平直径AB长度为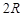
，现将质量也为的小球从距A点正上方
高处由静止释放，然后由A点经过半圆轨道后从B冲出，在空中能上升的最大高度为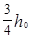
（不计空气阻力），则（ ）
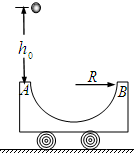
| A．小球和小车组成的系统动量守恒 |
B．小车向左运动的最大距离为 |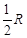
| C．小球离开小车后做斜上抛运动 |
D．小球第二次能上升的最大高度 |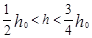
在足够高的空间内，小球位于空心管的正上方h处，空心管长为L，小球球心与管的轴线重合，并在竖直线上，释放小球，小球可能穿过空心管，不计空气阻力，则下列判断正确的是（ ）
| A．两者均无初速度同时释放，小球在空中不能穿过管 |
| B．两者同时释放，小球具有竖直向下的初速度v0，管无初速度，则小球一定能穿过管，且穿过管的时间与当地重力加速度无关 |
| C．两者同时释放，小球具有竖直向下的初速度v0，管无初速度，则小球一定能穿过管，且穿过管的时间与当地重力加速度有关 |
D．两者均无初速度释放，但小球提前了 时间释放，则小球一定能穿过管，但穿过管的时间与当地重力加速度有关 |
如图所示，在一个桌面上有三个金属小球A.B.c，离桌面高度分别为h1∶h2∶h3=3∶2∶1．若先后顺次释放A.B.c，三球刚好同时落到桌面上，不计空气阻力，则（ ）
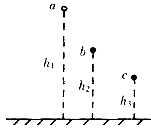
A.三者到达桌面时的速度之比是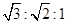
B.三者运动时间之比为3∶2∶1
C.b与a开始下落的时间差小于c与开始下落的时间差
D.三个小球运动的加速度与小球受到的重力成正比，与质量成反比
某同学为估测一教学楼的总高度，在楼顶将一直径为2cm的钢球由静止释放，测得通过安装在地面的光电门数字计时器的时间为0.001s，由此可知教学楼的总高度约为（不计空气阻力，重力加速度g取10m/s2）（ ）
| A．10m | B．20m | C．30m | D．40m |
伽利略文理研究自由落体得有点规律，将落体实验转化为著名的“斜面实验”，对于这个研究过程，下列说法正确的是（ ）
| A．斜面实验是一个理想实验 |
| B．斜面实验放大了重力的作用，便于测量小球运动的路程 |
| C．不直接做落体实验是因为当时时间测量不够精确 |
| D．通过对斜面实验的观察与计算，直接得到落体运动的规律 |
物体从离地面45 m高处做自由落体运动（g取10 m/s2），则下列选项中正确的是（ ）
| A．物体运动3 s后落地 |
| B．物体落地时的速度大小为30 m/s |
| C．物体在落地前最后1 s内的位移为25 m |
| D．物体在整个下落过程中的平均速度为20 m/s |
将自由落体运动分成时间相等的4段，物体通过最后1段时间下落的高度为56 m，那么物体下落的第1段时间所下落的高度为（ ）
| A．3.5 m | B．7 m | C．8 m | D．16 m |
试题篮
()
粤公网安备 44130202000953号
代表动能，
代表势能，
代表下落的距离，以水平地面为零势能面。下列所示图像中，能正确反映各物理量之间关系的是（ ）
落地，则当它下落
时，离地面的高度为（ ）
