下列关于点电荷的叙述正确的是( )
| A.点电荷就是电荷量和体积都是足够小的带电体 |
| B.体积大,形状怪异的带电体一定不能视为点电荷 |
C.点电荷所带电量的绝对值为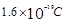 |
| D.带电体的形状和大小对其库仑力的影响可忽略时,带电体可看作点电荷 |
下列关于静电场的说法正确的是( )
| A.在孤立点电荷形成的电场中没有场强相同的两点,但有电势相同的两点 |
| B.正电荷只在电场力作用下,一定从高电势向低电势运动 |
| C.场强为零处,电势一定为零;电势为零处,场强不一定为零 |
| D.初速为零的正电荷在电场力作用下一定沿电场线运动 |
一金属杆ab,以某一初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成θ角,两导轨上端用一电阻R相连,如图所示.匀强磁场垂直斜面向上,导轨与杆的电阻以及它们之间的接触电阻均不计,金属杆向上滑行到某一高度之后又返回到底端,则在此全过程中( )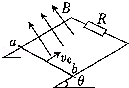
| A.向上滑行的时间大于向下滑行的时间 |
| B.向上滑行过程中克服安培力做的功大于向下滑行过程中克服安培力做的功 |
| C.向上滑行过程中电阻R上产生的热量等于向下滑行过程中电阻R上产生的热量 |
| D.向上滑行过程中通过电阻R的电荷量等于向下滑行过程中通过电阻R的电荷量 |
科学家在研究原子、原子核及基本粒子时,为了方便,常常用元电荷作为电量的单位,关于元电荷,下列说法中不正确的是( )
| A.把质子或电子叫元电荷 |
| B.1.60×10-19C的电量叫元电荷 |
| C.电子带有最小的负电荷,其电量的绝对值叫元电荷 |
| D.质子带有最小的正电荷,其电量的绝对值叫元电荷 |
关于元电荷,下列说法中错误的是( )
| A.元电荷实质是指电子和质子本身 |
| B.所有带电体的电荷量一定等于元电荷的整数倍 |
| C.元电荷的值通常取作e=1.60×10﹣19C |
| D.电荷量e的数值最早是由美国科学家密立根用实验测得的 |
下列实验中准确测定元电荷电量的实验是( )
| A.库仑扭秤实验 | B.密立根油滴实验 |
| C.用DIS描绘电场的等势线实验 | D.奥斯特电流磁效应实验 |
两个完全相同的金属小球A、B,球A所带电荷量为+4Q,球B不带电.现将球B与球A接触后,移到与球A相距为d处(d远远大于小球半径).已知静电力常量为k,则此时两球A、B之间相互作用的库仑力大小是( )
A.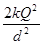 B.
B.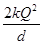 C.
C.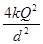 D.
D.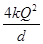 .
.
富兰克林是根据带电体间的相互作用,发现电荷有正、负两种,如图所示,绝缘细线上端固定,下端悬挂一轻质小球a,a的表面镀有铝膜,在a的近旁有一固定绝缘金属球b,则( )
| A.若a顺时针摆动,证明a、b带同种电荷 |
| B.若a逆时针摆动,证明a、b带异种电荷 |
| C.若a顺时针摆动,证明a、b带异种电荷 |
| D.若a逆时针摆动,证明a、b带同种电荷 |
某同学为检验某空间有无电场或者磁场存在,想到的以下方法中可行的是( )
| A.在该空间内引入检验电荷,如果电荷受到电场力说明此空间存在电场 |
| B.在该空间内引入检验电荷,如果电荷没有受到电场力说明此空间不存在电场 |
| C.在该空间内引入通电导线,如果通电导线受到磁场力说明此空间存在磁场 |
| D.在该空间内引入通电导线,如果通电导线没有受到磁场力说明此空间不存在磁场 |
如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )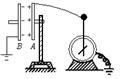
| A.将B板稍微向右移,静电计指针张角将变小 |
| B.若将B板稍微向上移,静电计指针张角将变小 |
| C.若将B板拿走,静电计指针张角变为零 |
| D.若将玻璃板插入两极板之间,静电计指针张角将变大 |
有两个完全相同的金属球A、B,B球固定在绝缘地板上,A球在离B球为H的正上方由静止释放下落,与B球发生对心正碰后回跳的高度为h.设碰撞中无动能损失,空气阻力不计,若( )
A.A、B球带等量同种电荷,则h>H
B.A、B球带等量同种电荷,则h=H
C.A、B球带等量异种电荷,则h>H
D.A、B球带等量异种电荷,则h=H
下列表述正确的是
| A.库仑发现了点电荷间相互作用规律 |
| B.法拉第最早引入了电场概念,并提出用电场线表示电场 |
| C.行星在圆周轨道上保持匀速率运动的性质是惯性 |
| D.安培发现了磁场对运动电荷的作用规律 |
下列关于点电荷的说法,正确的是
| A.只有体积很小的带电体才可看成点电荷 |
| B.体积很大的带电体一定不是点电荷 |
| C.任何带电体,都可以看成是电荷全部集中于球心的点电荷 |
| D.当两个带电体的形状和大小对相互作用力的影响可忽略时,它们可看成点电荷 |
关于点电荷和元电荷的说法中,正确的是:
| A.只有很小的球形带电体才叫做点电荷 |
| B.带电体间的距离比它们本身的大小大得多,以至带电体的形状和大小对它们之间的作用力影响可以忽略不计时,带电体就可以视为点电荷 |
| C.元电荷就是电子 |
| D.任何带电体的电量都是元电荷的整数倍 |
试题篮
()