如图所示是医用回旋加速器示意图,其核心部分是两个D形金属盒,两金属盒置于匀强磁场中,并分别与高频电源相连。现分别加速氘核( )和氦核(
)和氦核( )。下列说法中正确的是( )
)。下列说法中正确的是( )
| A.它们的最大速度相同 |
| B.它们的最大动能相同 |
| C.它们在D形盒中运动的周期相同 |
| D.仅增大高频电源的电压可增大粒子的最大动能 |
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交变电流源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子时,匀强磁场的磁感应强度为B,高频交变电压频率为f.则下列说法正确的是( )
| A.质子被加速后的最大速度不可能超过2πfR |
| B.质子被加速后的最大速度与加速电场的电压大小无关 |
| C.只要R足够大,质子的速度可以被加速到任意值 |
| D.不改变B和f,该回旋加速器也能用于加速α粒子 |
飞行时间质谱仪可对气体分子进行分析。如图所示,在真空状态下,脉冲阀P喷出微量气体,经激光照射产生电荷量为q、质量为m的正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的偏转控制区,到达探测器。已知a、b板间距为d,极板M、N的长度和间距均为L。不计离子重力及进入a板时的初速度。
(1)当a、b间的电压为U1,在M、N间加上适当的电压U2,使离子到达探测器。求离子到达探测器的全部飞行时间。
(2)为保证离子不打在极板上,试求U2与U1的关系。
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为 .若用回旋加速器加速质子(氢核)时,匀强磁场的磁感应强度为
.若用回旋加速器加速质子(氢核)时,匀强磁场的磁感应强度为 ,高频交流电的频率为
,高频交流电的频率为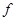 .质子质量为
.质子质量为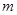 ,电荷量为
,电荷量为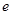 .则下列说法正确的是 ( )
.则下列说法正确的是 ( )
A.高频交流电频率应为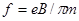 |
B.质子被加速后的最大动能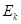 不可能超过 不可能超过 |
| C.质子被加速后的最大动能与狭缝间的加速电压、加速次数有关 |
D.不改变 和 和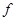 ,该回旋加速器也能用于加速 ,该回旋加速器也能用于加速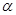 粒子(即氦核) 粒子(即氦核) |
美国物理学家劳伦斯于1932年发明的回旋加速器,应用带电粒子在磁场中做圆周运动的特点,能使粒子在较小的空间范围内经过电场的多次加速获得较大的能量,使人类在获得高能量带电粒子方面前进了一步.如图为一种改进后的回旋加速器示意图,其中盒缝间的加速电场场强大小恒定,且被限制在A、C板间,如图所示.带电粒子从P0处以速度v0沿电场线方向射入加速电场,经加速后再进入D形盒中的匀强磁场做匀速圆周运动.对于这种改进后的回旋加速器,下列说法正确的是( )
A.带电粒子每运动一周被加速两次
B.带电粒子每运动一周P1P2=P2P3
C.加速电场方向需要做周期性的变化
D.加速粒子的最大速度与D形盒的尺寸有关
1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示.这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,下列说法正确的是( )
| A.离子由加速器的中心附近进入加速器 |
| B.离子由加速器的边缘进入加速器 |
| C.离子从磁场中获得能量 |
| D.离子从电场中获得能量 |
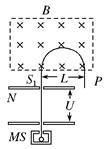
如图所示,离子源S产生质量为m,电荷量为q的离子,离子产生出来的速度很小,要以看做速度为0,产生的离子经过电压U加速后,进入磁感强度为B的一匀强磁场,沿着半圆周运动到达P点,测得P点到入口处S1的距离为L,则 N极板为________极板,此离子荷质比 =_____________.
=_____________.
环形对撞机是研究高能粒子的重要装置,其核心部件是一个高度真空的圆环状的空腔.若带电粒子初速度可视为零,经电压为U的电场加速后,沿圆环切线方向注入对撞机的环状空腔内,空腔内存在着与圆环平面垂直的匀强磁场,磁感应强度大小为B.带电粒子将被限制在圆环状空腔内运动.要维持带电粒子在圆环内做半径确定的圆周运动,下列说法中正确的是( )
A.对于给定的加速电压,带电粒子的比荷q/m越大,磁感应强度B越大
B.对于给定的加速电压,带电粒子的比荷q/m越大,磁感应强度B越小
C.对于给定的带电粒子和磁感应强度B,加速电压U越大,粒子运动的周期越小
D.对于给定的带电粒子和磁感应强度B,不管加速电压U多大,粒子运动的周期都不变
(17分)(2009·江苏高考)1932年,劳伦斯和利文斯顿设计出了回旋加速器.回旋加速器的工作原理如图17所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计,磁感应强度为B的匀强磁场与盒面垂直,A处粒子源产生的粒子,质量为m,电荷量为+q,在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用.
(1)求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比;
(2)求粒子从静止开始加速到出口处所需的时间t;
(3)实际使用中,磁感应强度和加速电场频率都有最大值的限制.若某一加速器磁感应
强度和加速电场频率的最大值分别为Bm、fm,试讨论粒子能获得的最大动能Ekm.
(12分)如图14所示,回旋加速器D形盒的半径为R,用来加速质量为m、电荷量为q的质子,使质子由静止加速到能量为E后,由A孔射出,求:
(1)加速器中匀强磁场B的方向和大小;
(2)设两D形盒间距为d,其间电压为U,电场视为匀强电场,质子每次经电
场加速后能量增加,加速到上述能量所需回旋周数;
(3)加速到上述能量所需时间.
回旋加速器是用来加速带电粒子的装置,如图1所示.它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(13H)和α粒子(24He),比较它们所加的高频交流电源的周期和获得的最大动能的大小,有 ( )
| A.加速氚核的交流电源的周期较大,氚核获得的最大动能也较大 |
| B.加速氚核的交流电源的周期较大,氚核获得的最大动能较小 |
| C.加速氚核的交流电源的周期较小,氚核获得的最大动能也较小 |
| D.加速氚核的交流电源的周期较小,氚核获得的最大动能较大 |
回旋加速器是加速带电粒子的装置.其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( ) 
| A.减小磁场的磁感应强度 |
| B.增大匀强电场间的加速电压 |
| C.增大D形金属盒的半径 |
| D.减小狭缝间的距离 |
12.图是质谱仪的工作原理示意图。带电粒子被加速电场加速后,进入速度选择器。速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B和E。平板S上有可让粒子通过的狭缝P和记录粒子位置的胶片A1A2。平板S下方有强度为B0的匀强磁场。下列表述正确的是( ) 
| A.质谱仪是分析同位素的重要工具 |
| B.速度选择器中的磁场方向垂直纸面向外 |
| C.能通过的狭缝P的带电粒子的速率等于E/B |
| D.粒子打在胶片上的位置越靠近狭缝P,粒子的荷质比越小 |
如图所示,有一半径为R1=1m的圆形磁场区域,圆心为O,另有一外半径为R2=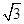 m、内半径为R1的同心环形磁场区域,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面,一带正电粒子从平行极板下板P点静止释放,经加速后通过上板小孔Q,垂直进入环形磁场区域,已知点P、Q、O在同一竖直线上,上极板与环形磁场外边界相切,粒子比荷q/m=4×107C/kg,不计粒子的重力,且不考虑粒子的相对论效应,求:
m、内半径为R1的同心环形磁场区域,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面,一带正电粒子从平行极板下板P点静止释放,经加速后通过上板小孔Q,垂直进入环形磁场区域,已知点P、Q、O在同一竖直线上,上极板与环形磁场外边界相切,粒子比荷q/m=4×107C/kg,不计粒子的重力,且不考虑粒子的相对论效应,求:
(1)若加速电压U1=1.25×102V,则粒子刚进入环形磁场时的速度 多大?
多大?
(2)要使粒子不能进入中间的圆形磁场区域,加速电压U2应满足什么条件?
(3)若改变加速电压大小,可使粒子进入圆形磁场区域,且能水平通过圆心O,最后返回到出发点,则粒子从Q孔进入磁场到第一次经过O点所用的时间为多少?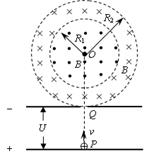
质谱议的构造原理如图所示.从粒子源S出来时的粒子速度很小,可以看作初速为零,粒子经过电场加速后进入有界的垂直纸面向里的匀强磁场区域,并沿着半圆周运动而达到照相底片上的P点,测得P点到入口的距离为x,则以下说法正确的是
| A.粒子一定带正电 |
| B.粒子一定带负电 |
| C.x越大,则粒子的质量与电量之比一定越大 |
| D.x越大,则粒子的质量与电量之比一定越小 |
试题篮
()