高中物理电磁场试题

如图所示，粒子源S可以不断地产生质量为m、电荷量为+q的粒子(重力不计)．粒子从O₁孔漂进(初速不计)一个水平方向的加速电场，再经小孔O₂进入相互正交的匀强电场和匀强磁场区域，电场强度大小为E，磁感应强度大小为B₁，方向如图．虚线PQ、MN之间存在着水平向右的匀强磁场，磁感应强度大小为B₂(图中未画出)．有一块折成直角的硬质塑料板abc(不带电，宽度很窄，厚度不计)放置在PQ、MN之间(截面图如图)，a、c两点恰在分别位于PQ、MN上，ab=bc=L，α= 45°．现使粒子能沿图中虚线O₂O₃进入PQ、MN之间的区域．
(1) 求加速电压U₁．
(2)假设粒子与硬质塑料板相碰后，速度大小不变，方向变化遵守光的反射定律．粒子在PQ、MN之间的区域中运动的时间和路程分别是多少？

如图16－101所示，电源电动势E＝2V，r＝0.5Ω，竖直导轨宽L＝0.2m，导轨电阻不计．另有一金属棒质量m＝0.1kg、电阻R＝0.5Ω，它与导轨间的动摩擦因数μ＝0.4，靠在导轨的外面．为使金属棒不滑，施一与纸面夹角为30°且与导体棒垂直指向纸里的匀强磁场，(设最大静摩擦力等于滑动摩擦力，取g＝10m/s2)．求：
(1)此磁场的方向．
(2)磁感强度B的取值范围．

如图所示，在平行竖直虚线a与b、b与c、c与d之间分别存在着垂直于虚线的匀强电场、平行于虚线的匀强电场、垂直纸面向里的匀强磁场,虚线d处有一荧光屏。大量正离子(初速度和重力均忽略不计）从虚线a上的P孔处进入左边电场,经过三个场区后有一部分打在荧光屏上。关于这部分离子,若比荷越大,则离子

A.经过虚线e的位置越低        B 经过虚线C的速度越大
C. 打在荧光屏上的位置越低    D.   打在荧光屏上的位置越高

如图所示，一块长为b，宽为a，厚为h=0.1mm的铜片，放在B=1.5T的匀强磁场中，磁场方向与铜片表面垂直．若铜片中通有自左向右的I=2A的电流时，铜片前后两侧面会形成一个电势差．金属导线中电流I与自由电子定向移动速度v、导线横截面积S间存在关系I=neSv，式中n为单位体积内的自由电子个数，若每个金属导体中每个原子仅提供一个自由电子(即自由电子数与金属内所含原子数相同)，试求：

(1)铜片前后侧面哪一面电势高?电势差为多少?
(2)在磁场和电流不变的条件下，如何改变金属片尺寸，可以增大该电势差?
(铜的密度近似为9.0×，铜的原子量近似为60，阿伏伽德罗常数为6.0×，电子电量为1.6×C)

如图是质谱仪的工作原理示意图。带电粒子被加速电场加速后，进入速度选择器。速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B和E．平板S上有可让粒子通过的狭缝P和记录粒子位置的胶片A₁A₂．平板S下方有磁感应强度为B₀的匀强磁场。下列表述正确的是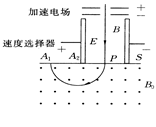

A．质谱仪是分析同位素的重要工具

B．速度选择器中的磁场方向垂直纸面向里

C．能通过狭缝P的带电粒子的速率等于E/B

D．粒子打在胶片上的位置越靠近狭缝P，粒子的比荷（q/m）越大

某空间存在着变化的电场和另一变化的磁场，电场方向向右，即图中由b点到c点的方向，电场强度大小变化如图中E-t图像，磁感强度变化如图中B-t图像。已知ab垂直于bc，，在a点，从第1s末时刻开始，每隔2s有一相同带电粒子（粒子重力不计）沿ab方向以速度v射出，这些粒

子都恰能击中c点，且粒子在ac间运动时间小于1s，求：
(1)图像中E₀和B₀的比值。
(2)第二个粒子和第一个粒子从射出到击中c点所用时间的比值。

在直角坐标xoy内，在第1象限的区域Ⅰ内存在垂直于纸面向外宽度为d的匀强磁场，区域Ⅱ内存在垂直于直面向里宽度为的匀强磁场；在第三象限存在沿Y轴正向的匀强电场，一质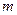量为带电量为的带电粒子从电场中的坐标为（-2h,-h）点以速度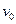水平向右射出，经过原点O处射入区域Ⅰ后垂直MN射入区域Ⅱ，（粒子的重力忽略不计）求：

（1）区域Ⅰ内磁感应强度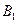的大小；
（2）若区域Ⅱ内磁感应强度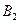的大小是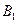的整数倍，当粒子再次回到MN时坐标可能值为多少？

如图中，XOZ是光滑水平面；空间有沿+Z方向的匀强磁场，其磁感强度为B。现有两块平行金属板，彼此间距为d，构成一个电容为C的平行板电容器；在两板之间焊一根垂直两板的金属杆PP'，已知两板和杆PP'的总质量为m，若对此杆PP'作用一个沿+X方向的恒力F，试推求此装置匀加速平移的加速度a的表达式。（用B、c、d、m、F等表示）

如图，与水平面成角的平面将空间分成I和II两个区域。一质量为、电荷量为（q＞0）的粒子以速度从平面上的点水平右射入I区。粒子在I区运动时，只受到大小不变、方向竖直向下的电场作用，电场强度大小为；在II区运动时，只受到匀强磁场的作用，磁感应强度大小为，方向垂直于纸面向里。求粒子首次从II区离开时到出发点的距离。(粒子的重力可以忽略)

。

三个速度大小不同而质量相同的一价离子，从长方形区域的匀强磁场上边缘平行于磁场边界射入磁场，它们从下边缘飞出时的速度方向见右图。以下判断正确的是（   ）

A．三个离子均带负电	B．三个离子均带正电
C．离子1在磁场中运动的轨道半径最大	D．离子3在磁场中运动的时间最长

下列说法中正确的是（    ）

A．检验电荷在某处不受电场力的作用，则该处电场强度不一定为零

B．一小段通电导线在某处不受磁场力作用，则该处磁感应强度一定为零

C．表征电场中某点电场的强弱，是把一个检验电荷放在该点时受到的电场力与检验电荷本身电荷量的比值

D．表征磁场中某点磁场的强弱，是把一小段通电导线放到该点时受到的磁场力与该小段导线长度和电流乘积的比值

下列各图中，用带箭头的细实线表示通电直导线周围磁感线的分布情况，其中正确的是（　　）

地面附近，存在着一有界电场，边界MN将某空间分成上下两个区域Ⅰ、Ⅱ，在区域Ⅱ中有竖直向上的匀强电场，在区域Ⅰ中离边界某一高度由静止释放一质量为m的带电小球A，如图甲所示，小球运动的v－t图象如图乙所示，已知重力加速度为g，不计空气阻力，则

A．在t＝2.5s时，小球经过边界MN

B．小球受到的重力与电场力之比为3∶5

C．在小球向下运动的整个过程中，重力做的功与电场力做的功大小相等

D．在小球运动的整个过程中，小球的机械能与电势能总和先变大再变小

利用电场和磁场，可以将比荷不同的离子分开，这种方法在化学分析和原子核技术等领域有重要的应用。
如图所示的矩形区域（边足够长）中存在垂直于纸面的匀强磁场，处有一狭缝。离子源产生的离子，经静电场加速后穿过狭缝沿垂直于边且垂于磁场的方向射入磁场，运动到边，被相应的收集器收集，整个装置内部为真空。

已知被加速的两种正离子的质量分别是和，电荷量均为。加速电场的电势差为，离子进入电场时的初速度可以忽略。不计重力，也不考虑离子间的相互作用。

(1)求质量为的离子进入磁场时的速率。

(2)当磁感应强度的大小为时，求两种离子在边落点的间距。

(3)在前面的讨论中忽略了狭缝宽度的影响，实际装置中狭缝具有一定宽度。若狭缝过宽，可能使两束离子在边上的落点区域交叠，导致两种离子无法完全分离，设磁感应强度大小可调，边长为定值L，狭缝宽度为，狭缝右边缘在A处，离子可以从狭缝各处射入磁场，入射方向仍垂直于边且垂直于磁场。为保证上述两种离子能落在边上并被完全分离，求狭缝的最大宽度。

若粒子刚好能在如图所示的竖直面内做匀速圆周运动，则可以判断

A．粒子运动中机械能守恒	B．粒子带负电
C．只能是逆时针运动	D．只能是顺时针运动