高中物理链式反应及其发生条件计算题

如图13所示，水上滑梯由斜槽AB和水平槽BC构成，AB与BC圆滑连接，斜槽的竖直高度，BC面高出水面的距离。一质量m=50kg的游戏者从滑梯顶端A点由静止滑下，取10mol/s²。
（1）若忽略游戏者下滑过程中受到的一切阻力，求游戏者从斜槽顶端A点由静止滑下到斜槽底端B点的速度大小；
（2）若由于阻力的作用，游戏者从滑梯顶端A点由静止滑下到达滑梯末端C点时的速度大小=15m/s，求这一过程中游戏者克服阻力做的功；
（3）若游戏者滑到滑梯末端C点以=15m/s的速度水平飞出，求他从C点水平飞出到落入水中时，他在空中运动过程中水平方向的位移。

图为"嫦娥三号"探测器在月球上着陆最后阶段的示意图.首先在发动机作用下，探测器受到推力在距月球高度为处悬停（速度为，远小于月球半径）；接着推力改变，探测器开始竖直下降，到达距月面高度为处的速度为，此后发动机关闭，探测器仅受重力下落至月面.已知探测器总质量为（不包括燃料），地球和月球的半径比为，质量比为，地球表面附近的重力加速度为，求：

（1）月球表面附近的重力加速度大小及探测器刚接触月面时的速度大小；

（2）从开始竖直下降到刚接触月面时，探测器机械能的变化。

(9分)如图示，竖直平面内一光滑水平轨道左边与墙壁对接，右边与一足够高的1/4光滑圆弧轨道平滑相连，木块A、B静置于光滑水平轨道上，A、B质量分别为1.5kg和0.5kg。现让A以6m/s的速度水平向左运动，之后与墙壁碰撞，碰撞时间为0.3s，碰后速度大小变为4m/s。当A与B碰撞后会立即粘在一起运动，已知g=10m/s² 求 ：
①A与墙壁碰撞过程中，墙壁对小球平均作用力的大小；
②A、B滑上圆弧轨道的最大高度。

如图，水平轨道AB与半径为R="1.0" m的竖直半圆形光滑轨道BC相切于B点．可视为质点的a、b两个小滑块质量m_a=2m_b="2" kg，原来静止于水平轨道A处，AB长为L=3.2m，两滑块在足够大的内力作用下突然分开，已知a、b两滑块分别沿AB轨道向左右运动，v_a = 4.5m/s，b滑块与水平面间动摩擦因数，g取10m/s²．则
(1)小滑块b经过圆形轨道的B点时对轨道的压力．
(2)通过计算说明小滑块b能否到达圆形轨道的最高点C．

如图所示，三个可视为质点的滑块质量分别为m_A=m，m_B=2m，m_C=3m，放在光滑水平面上，三滑块均在同一直线上．一轻质弹簧的一端固定在滑块B上，另一端与滑块C接触但未连接，B、C均静止。现滑块A以速度v₀=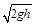与滑块B发生碰撞（碰撞时间极短）后粘在一起，并压缩弹簧推动滑块C向前运动，经一段时间，滑块C脱离弹簧，继续在水平面上匀速运动，求：

①被压缩弹簧的最大弹性势能
②滑块C脱离弹簧后A、B、C三者的速度

如图是为了检验某种防护罩承受冲击力的装置。M是半径为R=1.0m的固定于竖直平面内的1/4光滑圆弧轨道，轨道上端切线水平，N为待检验的固定曲面，该曲面在竖直面内的截面为半径的1/4圆弧，圆弧下端切线水平且圆心恰好位于M轨道的上端点，M的下端相切处放置竖直向上的弹簧枪，可发射速度不同的质量m=0.01kg的小钢珠。假设某次发射的钢珠沿轨道恰好能经过M的上端点，水平飞出后落到曲面N的某一点上，取g=10m/s²。求：

（1）发射该钢球前，弹簧的弹性势能E_P多大？
（2）钢珠从M圆弧轨道最高点飞出至落到圆弧N上所用的时间是多少？（结果保留两位有效数字）

如图所示，有一粗糙水平面AB与一光滑的、很长的斜面BC在B点平滑连接，M = 2kg的物体与水平面见的动摩擦因素µ=0.4，现使其从A点以V_A=8m/s的水平速度向B运动，S_AB=6m物体经过B点后沿斜面上滑，之后又回滑经过B点而停在水平面上。求：

(1)物体回到B点时的速度V_B.
(2)物体沿斜面上升的最大高度h
(3)物体停在水平面上的位置（用A点描述）

如图所示，一水平传送带始终保持着大小为v₀＝4m/s的速度做匀速运动。在传送带右侧有一半圆弧形的竖直放置的光滑圆弧轨道，其半径为R=0.2m，半圆弧形轨道最低点与传送带右端B衔接并相切，一小物块无初速地放到皮带左端A处，经传送带和竖直圆弧轨道至最高点C。已知当A、B之间距离为s=1m时，物块恰好能通过半圆轨道的最高点C，（g=10m/s²）则：

(1) 物块至最高点C的速度v为多少?
(2) 物块与皮带间的动摩擦因数为多少？
(3) 若只改变传送带的长度，使滑块滑至圆弧轨道的最高点C 时对轨道的压力最大，传送带的长度应满足什么条件？

距沙坑高h=7m处，以v₀=10m/s的初速度竖直向上抛出一个质量为0.5kg的物体，物体落到沙坑并陷入沙坑d=0.4m深处停下．不计空气阻力，重力加速度g=10m/s²．求：

（1）物体上升到最高点时离抛出点的高度H；
（2）物体在沙坑中受到的平均阻力f大小是多少？

两根长直轨道与一半径为R的半圆型圆弧轨道相接于A、C两点，B点为轨道最低点，O为圆心，轨道各处光滑且固定在竖直平面内。质量均为m的两小环P、Q用长为R的轻杆连接在一起，套在轨道上。将MN两环从距离地面2R处由静止释放，整个过程中轻杆和轨道始终不接触，重力加速度为g，求：
（1）当P环运动到B点时，系统减少的重力势能△E_P；
（2）当P环运动到B点时的速度v；
（3）在运动过程中，P环能达到的最大速度v_m；
（4）若将杆换成长，P环仍从原处由静止释放，经过半圆型底部再次上升后，P环能达到的最大高度H。

如图，质量分别为、的两个小球、静止在地面上方，球距地面的高度，球在球的正上方。 先将球释放，经过一段时间后再将球释放。 当球下落时，刚好与球在地面上方的点处相碰，碰撞时间极短，碰后瞬间球的速度恰为零。已知，重力加速度大小为。

（i）球第一次到达地面时的速度；

（ii）点距离地面的高度。

我国的月球探测计划“嫦娥工程”分为“绕、落、回”三步。“嫦娥三号”的任务是“落”。  2013年12月2日，“嫦娥三号”发射，经过中途轨道修正和近月制动之后，“嫦娥三号”探测器进入绕月的圆形轨道I。12月12日卫星成功变轨，进入远月点P、近月点Q的椭圆形轨道II。如图所示。 2013年12月14日，“嫦娥三号”探测器在Q点附近制动，由大功率发动机减速，以抛物线路径下降到距月面100米高处进行30s悬停避障，之后再缓慢竖直下降到距月面高度仅为数米处，为避免激起更多月尘，关闭发动机，做自由落体运动，落到月球表面。
已知引力常量为G，月球的质量为M，月球的半径为R，“嫦娥三号”在轨道I上运动时的质量为m， P、Q点距月球表面的高度分别为h₁、h₂。

（1）求“嫦娥三号”在圆形轨道I上运动的速度大小；
（2）已知“嫦娥三号”与月心的距离为r时，引力势能为（取无穷远处引力势能为零），其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中，动能和引力势能相互转化，它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v，请根据能量守恒定律求它经过P点时的速度大小；

如图所示，光滑固定的竖直杆上套有一个质量m=0．4 kg的小物块A，不可伸长的轻质细绳通过固定在墙壁上、大小可忽略的定滑轮D，连接小物块彳和小物块曰，虚线CD水平，间距d=1．2 m，此时连接小物块彳的细绳与竖直杆的夹角为37°，小物块彳恰能保持静止．现在在小物块B的下端挂一个小物块Q（未画出，小物块A可从图示位置上升并恰好能到达C处，不计摩擦和空气阻力，cos37°= 0．8、sin37°=0．6，重力加速度誊取l0m/s²．求：
（1）小物块A到达C处时的加速度大小；
（2）小物块B的质量；
（3）小物块Q的质量．

如图12所示,在同一竖直平面内两正对着的相同半圆光滑轨道，相隔一定的距离，虚线沿竖直方向，一小球能在其间运动，今在最低点与最高点各放一个压力传感器，测试小球对轨道的压力，并通过计算机显示出来，当轨道距离变化时，测得两点压力差与距离的图象如右下图所示。（不计空气阻力，g 取10 m/s²）求：
（1）小球的质量；
（2）相同半圆光滑轨道的半径；
（3）若小球在最低点B的速度为20m/s，为使小球能沿光滑轨道运动，求的最大值。

如图所示，A物体用板托着，位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连，绳子处于绷直状态，已知A物体质量M=1.5㎏，B物体质量m=1.0kg，现将板抽走,A将拉动B上升，设A与地面碰后不反弹，B上升过程中不会碰到定滑轮，问：B物体在上升过程中离地的最大高度为多大？取g =10m/s²．