高中物理研究电磁感应现象综合题

如图所示，由粗细均匀的电阻丝绕成的矩形导线框abcd固定于水平面上，导线框边长="L," =2L，整个线框处于竖直方向的匀强磁场中，磁场的磁感应强度为B，导线框上各段导线的电阻与其长度成正比，已知该种电阻丝单位长度上的电阻为，的单位是Ω/m．今在导线框上放置一个与ab边平行且与导线框接触良好的金属棒MN,MN的电阻为r，其材料与导线框的材料不同．金属棒MN在外力作用下沿x轴正方向做速度为v的匀速运动，在金属棒从导线框最左端（该处x=0)运动到导线框最右端的过程中：
(1)请写出金属棒中的感应电流I随x变化的函数关系式；
(2)试证明当金属棒运动到bc段中点时，MN两点间电压最大，并请写出最大电压U_m的表达式；
(3)试求出在此过程中，金属棒提供的最大电功率P_m；
(4)试讨论在此过程中，导线框上消耗的电功率可能的变化情况．

如图所示，两根平行金属导轨固定在水平桌面上，每根导轨每米的电阻为r₀=0.10Ω/m，导轨的端点P、Q用电阻可以忽略的导线相连，两导轨间的距离l=0.20m。有随时间变化的匀强磁场垂直于桌面，已知磁感应强度B与时间t的关系为B=kt，比例系数k=0.020T/s。一电阻不计的金属杆可在导轨上无摩擦低滑动，在滑动过程中保持与导轨垂直。在t=0时刻，金属杆紧靠在P、Q端，在外力作用下，杆以恒定的加速度从静止开始向导轨的另一端滑动，求在t=6.0s时金属杆所受的安培力。

如图甲所示，真空中两水平放置的平行金属板C、D，上面分别开有正对的小孔O₁、O₂，金属板C、D接在正弦交流电流上，两板C、D间的电压U_CD随时间t变化的图象如图乙所示．t=0时刻开始，从小孔O₁处不断飘入质量m="3." 2×10^-25kg、电荷量e="1." 6 ×10^-19C的带正电的粒子（设飘入速度很小，可视为零）．在D板外侧有以MN为边界的匀强磁场，MN与金属板心相距d="10" cm，匀强磁场的磁感应强度大小B="0." 1 T，方向如图甲所示，粒子的重力及粒子之间的相互作用力不计．平行金属板C、D之间的距离足够小，粒子在两板间的运动时间可以忽略不计．求：
(1)带电粒子经小孔O₂进入磁场后能飞出磁场边界MN的最小速度为多大？
(2)从0到0.04 s末的时间内，哪些时刻飘入小孔O₁的粒子能穿过电场并飞出磁场边界MN?
(3)磁场边界MN有粒子射出的长度范围．（保留一位有效数字）

图1是一台发电机定子中的磁场分布图，其中N、S是永久磁铁的两个磁极，它们的表面呈半圆柱面形状。M是圆柱形铁芯，它与磁极的柱面共轴。磁极与铁芯之间的缝隙中形成方向沿圆柱半径、大小近似均匀的磁场，磁感强度B＝0.050T
图2是该发电机转子的示意图(虚线表示定子的铁芯M)。矩形线框abcd可绕过ad、cb 边的中点并与图1中的铁芯M共轴的固定转轴oo′旋转，在旋转过程中，线框的ab、cd边始终处在图1所示的缝隙内的磁场中。已知ab边长 l₁＝25.0cm, ad边长 l₂＝10.0cm 线框共有N＝8匝导线，放置的角速度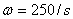。将发电机的输出端接入图中的装置K后，装置K能使交流电变成直流电，而不改变其电压的大小。直流电的另一个输出端与一可变电阻R相连，可变电阻的另一端P是直流电的正极，直流电的另一个输出端Q是它的负极。
图3是可用于测量阿伏加德罗常数的装置示意图，其中A、B是两块纯铜片，插在CuSO₄稀溶液中，铜片与引出导线相连，引出端分别为x、 y。
现把直流电的正、负极与两铜片的引线端相连，调节R，使CuSO₄溶液中产生I＝0.21A的电流。假设发电机的内阻可忽略不计，两铜片间的电阻r是恒定的。
（1）求每匝线圈中的感应电动势的大小。
（2）求可变电阻R与A、B间电阻r之和。

现代家庭电器化越来越高，用电安全是一个十分突出的问题．


(1)下表提供了一组部分人的人体电阻平均值数据：

①表中可看出干燥时电阻大约是潮湿时电阻的________倍．
②在空格中填入对人体加220V电压后的电流值．
(2)洗衣机的外壳是金属的(有许多地方没有油漆)，如图(a)表示插头没有接地线，外壳与相线(俗称火线)接触漏电，手触及外壳，试在图中画出电流通过的路线(假设此时M为正，N为负)．图(b)表示插头中的接地线，接在洗衣机外壳，此时发生漏电，试在此图中画出电流通过的路线．
(3)电路上有规格为10A熔丝(俗称保险丝)，如图(c)用电器R的功率是150W，这时通过熔丝实际电流是多少？一个潮湿的人，手脚触电，为什么熔丝不会断(即熔丝不能救人命)？
(4)图(d)是一种触电保安器，保安器A处用相线和零线双股平行绕制成线圈，然后接到用电器，B处有一个输出线圈，一旦线圈中有电流，经放大后便能推动继电器切断电源．
试说明：①为什么多开灯不会使保安器切断电源；②为什么有人“手地”触电保安器会切断电源；③该保安器能不能为双手“相线零线”触电保安？为什么？
③若人的安全电流是25mA以下，上述哪几项是十分危险的？
 

如图所示，长L="O." 80 m，电阻r="0." 30Ω，质量m="0." 10 kg的金属棒CD垂直放在水平导轨上，导轨由两条平行金属杆组成，已知金属杆表面光滑且电阻不计，导轨间距也是L，金属棒与导轨接触良好，量程为0～3. 0 A的电流表串联接在一条导轨上，在导轨左端接有阻值R="0." 50Ω的电阻，量程为0～1. 0 V的电压表接在电阻R两端，垂直于导轨平面的匀强磁场向下穿过导轨平面．现以向右恒定的外力F="1.6" N使金属棒向右运动，当金属棒以最大速度在导轨平面上匀速滑动时，观察到电路中的一个电表正好满偏，而另一个电表未满偏．
(1)试通过计算判断此满偏的电表是哪个表；
(2)求磁感应强度的大小；
(3)在金属棒CD达到最大速度后，撤去水平拉力F，求此后电阻R消耗的电能．

光滑平行金属导轨长L＝2m，二导轨间距d＝0.5m，轨道平面与水平面的夹角为θ＝30°，导轨上端接一阻值为R＝0.5 W的电阻，其余电阻不计，轨道所在空间有垂直轨道平面的匀强磁场，磁感应强度B＝1T．有一不计电阻的金属棒ab的质量m＝0.5kg，放在导轨最上端，如图所示．当ab棒从最上端由静止开始自由下滑，到达底端脱离轨道时，电阻R上产生的热量为Q＝1J，求：

（1）当棒的速度为v＝2 m/s时，它的加速度是多少？
（2）棒下滑的最大速度是多少？
（3）棒下滑过程中通过电阻R的最大电流是多少？

如图，在水平面上有两条平行导电导轨MN、PQ,导轨间距离为，匀强磁场垂直于导轨所在的平面（纸面）向里，磁感应强度的大小为B，两根金属杆1、2摆在导轨上，与导轨垂直，它们的质量和电阻分别为和,两杆与导轨接触良好，与导轨间的动摩擦因数为，已知：杆1被外力拖动，以恒定的速度沿导轨运动；达到稳定状态时，杆2也以恒定速度沿导轨运动，导轨的电阻可忽略，求此时杆2克服摩擦力做功的功率。
      

如图甲所示，真空中两水平放置的平行金属板C、D，上面分别开有正对的小孔O₁和O₂，金属板C、D接在正弦交流电源上，C、D两板间的电压随时间t变化的图线如图乙所示。t=0时刻开始，从D板小孔O₁处连续不断飘入质量为=3.2×10^-25kg、电荷量q=1.6×10^-19C的带正电的粒子(设飘入速度很小，可视为零)。在C板外侧有以MN为上边界、CM为左边界的匀强磁场，MN与C金属板相距d=10cm，O₂C的长度L=10cm，匀强磁场的大小为B=0.1T，方向如图甲所示，粒子的重力及粒子间相互作用力不计，平行金属板C、D之间的距离足够小，粒子在两板间的运动时间可忽略不计。求：
(1)带电粒子经小孔 O₂进入磁场后，能飞出磁场边界MN的最小速度为多大；
(2)从0s到0.04s末时间内哪些时间段飘入小孔O₁的粒子能穿过电场并飞出磁场边界MN；
(3)磁场边界MN有粒子射出的长度范围(计算结果保留一位有效数字)；
(4)在图中用阴影标出粒子可能经过的磁场区域。

如图所示，半径为a的圆形区域内有匀强磁场，磁感应强度B＝0.2T，磁场方向垂直纸面向里，半径为b的金属圆环与磁场同心地放置，磁场与环面垂直，其中a＝0.4m，b＝0.6m，金属环上分别接有灯、，两灯的电阻均为．一金属棒MN与金属环接触良好，棒与环的电阻均不计．
（1）若棒以的速率在环上向右匀速滑动，求棒滑过圆环直经的瞬间，MN中的电动势和流过的电流；
（2）撤去中间的金属棒MN，将右边的半圆环以为轴向上翻转90 ，若此后磁场随时间均匀变化，其变化率为T/s，求的功率．

图中MN和PQ为竖直方向的两平行长直金属导轨，间距l为0.40m，电阻不计。导轨所在平面与磁感应强度B为0.50T的匀强磁场垂直。质量m为6.0×10^-3kg、电阻为1.0Ω的金属杆ab始终垂直于导轨，并与其保持光滑接触。导轨两端分别接有滑动变阻器和阻值为3.0Ω的电阻R₁。当杆ab达到稳定状态时以速率v匀速下滑，整个电路消耗的电功率P为0.27W，重力加速度取10m/s²，试求速率v和滑动变阻器接入电路部分的阻值R₂。

在图甲中，直角坐标系xOy第1、3象限内有匀强磁场，第1象限内的磁感应强度大小为2B，第3象限内的磁感应强度大小为B，磁感应强度的方向均垂直于纸面向里．现将半径为l、圆心角为90⁰的扇形导线框OPQ以角速度绕O点在纸面内沿逆时针匀速转动，导线框回路电限为R.
(1)求导线框中感应电流的最大值．
(2)在图乙中画出导线框匀速转动一周的时间内感应电流I随时间t变化的图象．（规定与图甲中线框的位置相对应的时刻为t=0，逆时针方向的电流为正方向）
(3)求线框匀速转动一周产生的热量．

如图所示，在磁感应强度大小为B，方向垂直纸面向里的匀强磁场中，有一个质量为m、半径为r、电阻为R的均匀圆形导线圈，线圈平面跟磁场垂直（位于纸面内），线圈与磁场边缘（图中虚线）相切，切点为A，现在A点对线圈施加一个方向与磁场垂直，位于线圈平面内并跟磁场边界垂直的拉力F，将线圈以速度v匀速拉出磁场．以切点为坐标原点，以F的方向为正方向建立x轴，设拉出过程中某时刻线圈上的A点的坐标为x.
(1)写出力F的大小与x的关系式；
(2)在F－x图中定性画出F－x关系图线，写出最大值F₀的表达式．

如图所示为某一装置的俯视图，M、N为两个竖直放置的平行金属板，相距为0.4 m，L₁和L₂为与M、N平行的两根金属导轨（两导轨较细，与M、N上边棱处于同一水平面）,L₁与M以及L₂与N的间距都是0. 1 m，两导轨的电阻不计，其右端接有R="0." 3Ω的电阻．现有一长为0. 4 m、电阻为0.2Ω的均匀金属导体棒ab，棒上的a、b、c、d四点分别与M、 N、L₁、L₂接触良好，且金属棒ab与金属板M、N正交，整个装置放在竖直向下的匀强磁场中．今有一带正电粒子（不计重力）以v₀="7" m/s的初速度平行于极板水平入射．求当金属棒ab向何方向以多大速度运动时，可使带电粒子做匀速直线运动？

如图所示，两根水平平行固定的光滑金属导轨宽为L，足够长，在其上放里两根长也为L且与导轨垂直的金属棒ab和cd，它们的质量分别为2m、m，电阻阻值均为R（金属导轨及导线的电阻均可忽略不计），整个装置处在磁感应强度大小为B、方向竖直向下的匀强磁场中．
(1)现把金属棒ab锁定在导轨的左端，如图甲，对 cd施加与导轨平行的水平向右的恒力F，使金属棒cd向右沿导轨运动，当金属棒cd的运动状态稳定时，金属棒cd的运动速度是多大？
(2)若对金属棒ab解除锁定，如图乙，使金属棒cd获得瞬时水平向右的初速度v₀，当它们的运动状态达到稳定的过程中，流过金属棒ab的电量是多少？整个过程中ab和cd相对运动的位移是多大？