高中物理α粒子散射实验试题

如图所示，在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场，其边界过原点O和y轴上的点A（0，L）。一质量为m、电荷量为e的电子从A点以初速度v₀平行于x轴正方向射入磁场，并从x轴上的B点射出磁场，射出B点时的速度方向与x轴正方向的夹角为60°。求：

（1）匀强磁场的磁感应强度B的大小；
（2）电子在磁场中运动的时间t。

如图所示，在一个圆形区域内，两个方向相反且都垂直于纸面的匀强磁场分布在以直径A₂A₄为边界的两个半圆形区域Ⅰ、Ⅱ中，A₂A₄与A₁A₃的夹角为60°.一质量为m、带电量为＋q的粒子以某一速度从Ⅰ区的边缘点A₁处沿与A₁A₃成30°角的方向射入磁场，随后该粒子以垂直于A₂A₄的方向经过圆心O进入Ⅱ区，最后再从A₄处射出磁场．已知该粒子从射入到射出磁场所用的时间为t，求：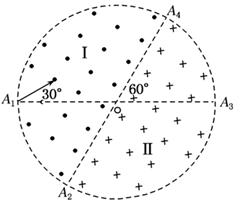

(1)画出粒子在磁场Ⅰ和Ⅱ中的运动轨迹；
(2)粒子在磁场Ⅰ和Ⅱ中的轨道半径R₁和R₂比值；
(3)Ⅰ区和Ⅱ区中磁感应强度的大小(忽略粒子重力)．

有一等腰直角ABC三角形区域，直角边长为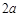。在该区域，有一垂直纸面向内磁感应强度为的匀强磁场。一束质量为、电荷量为，带负电粒子以不同速度从中点垂直直角边射入该磁场区域，在另一直角边放置一块荧光屏，如图所示。重力不计，求
（1）当粒子以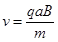入射时，求粒子在荧光屏上光斑的位置及在磁场中运动的时间。
（2）荧光屏AB区域上光斑的分布区域。
（3）若把磁场更换成沿AC方向的场强为E的匀强电场，当粒子以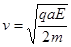入射时，求粒子在荧光屏上光斑的位置
（4）把磁场更换成沿AC方向的场强为E的匀强电场，荧光屏AB区域上光斑的分布区域。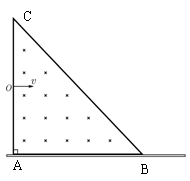

如图所示，有一个正方形的匀强磁场区域abcd，e是ad的中点，f是cd的中点，如果在a点沿对角线方向以速度v射入一带负电的带电粒子（带电粒子重力不计），恰好从e点射出，则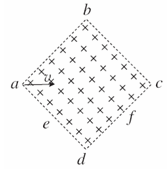

A．如果粒子的速度增大为原来的二倍，将从d点射出

B．如果粒子的速度增大为原来的三倍，将从f点射出

C．如果粒子的速度不变，磁场的磁感应强度变为原来的二倍，也将从d点射出

D．只改变粒子的速度使其分别从e、d、f点射出时，从e点射出所用时间最短

如图所示，水平放置的平行板电容器间有垂直纸面向里的匀强磁场，开关S闭合时一带电粒子恰好水平向右匀速穿过两板，重力不计。对相同状态入射的粒子，下列说法正确的是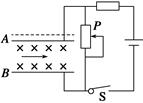

A．保持开关闭合，若滑片P向上滑动，粒子不可能从极板边缘射出

B．保持开关闭合，若滑片P向下滑动，粒子不可能从极板边缘射出

C．保持开关闭合，若A极板向上移动后，调节滑片P的位置，粒子仍可能沿直线射出

D．如果开关断开，粒子继续沿直线射出

如图所示，xOy坐标平面在竖直面内，x轴沿水平方向，y轴正方向竖直向上，在图示空间内有垂直于xOy平面的水平匀强磁场．一带电小球从O点由静止释放，运动轨迹如图中曲线．关于带电小球的运动，下列说法中正确的是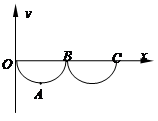

A．OAB轨迹为半圆

B．小球运动至最低点A时速度最大，且沿水平方向

C．小球在整个运动过程中机械能增加

D．小球在A点时受到的洛伦兹力与重力大小相等

图为可测定比荷的某装置的简化示意图，在第一象限区域内有垂直于纸面向里的匀强磁场，磁感应强度大小B=2.0×10^-3T，在X轴上距坐标原点L=0.50m的P处为离子的入射口，在Y轴上安放接收器，现将一带正电荷的粒子以v=3.5×10⁴m/s的速率从P处射入磁场，若粒子在y轴上距坐标原点L=0.50m的M处被观测到，且运动轨迹半径恰好最小，设带电粒子的质量为m,电量为q, 不计其重力。则上述粒子的比荷（C/kg） 是

A．

B．4.9×

C．

D．

质量和电量都相等的带电粒子M和N，以不同的速率经小孔S垂直进入匀强磁场，运行的半圆轨迹如图两种虚线所示，下列表述正确的是(  )[

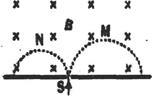
A．M带负电，N带正电

B．M的速率小于N的速率

C．洛伦兹力对M、N做正功

D．M的运行时间大于N的运行时间

如图所示，在x轴上方存在垂直于纸面向里的足够宽的匀强磁场，磁感应强度为B。在xoy平面内，从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计)．则下列说法正确的是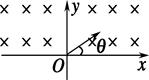

A．若v一定，θ越大，则粒子在磁场中运动的时间越短
B．若v一定，θ越大，则粒子在离开磁场的位置距O点越远
C．若θ一定，v越大，则粒子在磁场中运动的角速度越大
D．若θ一定，v越大，则粒子在磁场中运动的时间越短

如图所示，在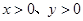的空间中有恒定的匀强磁场，磁感强度的方向垂直于Oxy平面向里，大小为B。现有一质量为m电量为q的带电粒子（不计重力），在x轴上到原点的距离为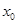的P点，以平行于y轴的初速度射入此磁场，在磁场力作用下沿垂直于y轴的方向射出此磁场。由这些条件可知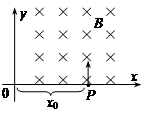

A．带电粒子一定带正电
B．不能确定粒子速度的大小
C．不能确定粒子射出此磁场的位置
D．不能确定粒子在此磁场中运动所经历的时间

如图所示，电子显像管由电子枪、加速电场、偏转磁场及荧光屏组成。在加速电场右侧有相距为D.长为L的两平板，两平板构成的矩形区域内存在方向垂直纸面向外的匀强磁场，磁场的右边界与荧光屏之间的距离也为d。荧光屏中点O与加速电极上两小孔S₁、S₂位于两板的中线上。从电子枪发射质量为m、电荷量为 –e的电子，经恒定电压为U₀的加速电场后从小孔S₂射出，经磁场偏转后，最后打到荧光屏上。若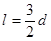，不计电子在进入加速电场前的速度。

（1）求电子进入磁场时的速度大小；
（2）电子到达荧光屏的位置与O点距离有最大值，求此时磁感应强度B的大小；

如图（甲）所示，某粒子源向外放射出一个α粒子，粒子速度方向与水平成30°角，质量为m，电荷量为+q。现让其从粒子源射出后沿半径方向射入一个磁感应强度为B、区域为圆形的匀强磁场（区域Ⅰ）。经该磁场偏转后，它恰好能够沿y轴进入下方的平行板电容器，并运动至N板且恰好不会从N板的小孔P射出电容器。已知平行板电容器与一边长为L的正方形单匝导线框相连，其内有垂直框面的磁场（区域Ⅱ），磁场变化如图（乙）所示。不计粒子重力，求：

（1）磁场区域Ⅱ磁场的方向及α粒子射出粒子源的速度大小；
（2）圆形磁场区域的半径；
（3）α粒子在磁场中运动的总时间。

在xOy平面上以O为圆心、半径为r的圆形区域内，存在磁感应强度为B的匀强磁场，磁场方向垂直于xOy平面．一个质量为m、电荷量为q的带电粒子，从原点O以初速度v沿y轴正方向开始运动，经时间t后经过x轴上的P点，此时速度与x轴正方向成θ角，如图所示．不计重力的影响，则下列关系一定成立的是（ ）．

A．若r<，则0°<θ<90°	B．若r≥，则t≥
C．若t＝，则r＝	D．若r＝，则t＝

如图是某屏蔽高能粒子辐射的装置，铅盒左侧面中心O有一放射源可通过铅盒右侧面的狭缝MQ向外辐射粒子，铅盒右侧有一左右边界平行的匀强磁场区域。过O的截面MNPQ位于垂直磁场的平面内，OH垂直于MQ。已知α粒子质量m=6.64×10^-27kg，电量q=3.20×10^-19C，速率v=1.28×10⁷m/s；磁场的磁感应强度B="0.664" T，方向垂直于纸面向里；粒子重力不计，忽略粒子间的相互作用及相对论效应，sin 53⁰ ="0." 8,cos 53⁰=0.60

（1）求垂直于磁场边界向左射出磁场的粒子在磁场中运动的时间t;
（2）若所有粒子均不能从磁场右边界穿出，达到屏蔽作用，求磁场区域的最小宽度d;
（3）求满足（2）条件的所有粒子在磁场中运动的最长时间和最短时间的比值t_max:t_min。

如图所示，MN是磁感应强度为B的匀强磁场的边界．一质量为m、电荷量为q的粒子在纸面内从O点射入磁场．若粒子速度为v₀，最远能落在边界上的A点．下列说法正确的有（ ）

A．若粒子落在A点的左侧，其速度一定小于v0

B．若粒子落在A点的右侧，其速度一定大于v0

C．若粒子落在A点左右两侧d的范围内，其速度不可能小于v0－

D．若粒子落在A点左右两侧d的范围内，其速度不可能大于v0＋