如图所示,匀强电场场强E=4V/m,方向水平向左,匀强磁场的磁感应强度B=2T,方向垂直纸面向里。质量m=1kg的带正电小物体A,从M点沿粗糙、绝缘的竖直墙壁无初速下滑,它滑行h=0.8m到N点时脱离墙壁做曲线运动,在通过P点瞬时,A受力平衡,此时其速度与水平方向成θ=45°角,且P点与M点的高度差为H=1.6m,当地重力加速度g取10m/s2。求:
(1)A沿墙壁下滑时,克服摩擦力做的功Wf;
(2)P点与M点的水平距离s。
如图所示,一电子(质量为m,电量绝对值为e)处于电压为U的水平加速电场的左极板A内侧,在电场力作用下由静止开始运动,然后穿过极板B中间的小孔在距水平极板M、N等距处垂直进入板间的匀强偏转电场。若偏转电场的两极板间距为d,板长为l,求:
(1)电子刚进入偏转电场时的速度v0;
(2)要使电子能从平行极板M、N间飞出,两个极板间所能加的最大偏转电压Umax′。
如图所示电路,R3=12Ω,当滑动变阻器R1调到6Ω时,电源的总功率为P=63W,输出功率为P出=54W,电源的内电阻为r=1Ω。求电源电动势E和流过滑动变阻器R1的电流I1。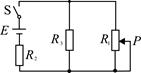
相距L="1.5" m的足够长金属导轨竖直放置,质量为m1=1kg的金属棒 和质量
和质量
为m2="0.27kg" 的金属棒cd均通过棒两端的套环水平地套在金属导轨上,如图(a)所示,虚线上方磁场方向垂直纸面向里,虚线下方磁场方问竖直向下,两处磁场磁感应强度大小相同。 棒光滑,cd棒与导轨间的动摩擦因数为
棒光滑,cd棒与导轨间的动摩擦因数为 ,两棒总电阻为1.8Ω,导轨电阻不计。ab棒在方向竖直向上,大小按图(b)所示规律变化的外力F作用下,从静止开始,沿导轨匀加速运动,同时cd捧也由静止释放。(
,两棒总电阻为1.8Ω,导轨电阻不计。ab棒在方向竖直向上,大小按图(b)所示规律变化的外力F作用下,从静止开始,沿导轨匀加速运动,同时cd捧也由静止释放。( 取10m/s2)
取10m/s2) 
(1)求出磁感应强度B的大小和ab棒加速度的大小;
(2)已知在2s内外力F做功40J,求这一过程中两金属棒产生的总焦耳热;
(3)判断cd棒将做怎样的运动,求出cd棒达到最大速度所需的时间 ,并在图(c)中定性画出cd棒所受摩擦力
,并在图(c)中定性画出cd棒所受摩擦力 随时间变化的图像。
随时间变化的图像。
平面直角坐标系 中,第1象限存在沿
中,第1象限存在沿 轴负方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度大小为B。一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度
轴负方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度大小为B。一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度 垂直于
垂直于 轴射入电场,经
轴射入电场,经 轴上的N点与
轴上的N点与 轴正方向成60º角射入磁场,最后从
轴正方向成60º角射入磁场,最后从 轴负半轴上的P点与
轴负半轴上的P点与 轴正方向成60º角射出磁场,如图所示。不计粒子重力,求:
轴正方向成60º角射出磁场,如图所示。不计粒子重力,求:

(1)粒子在磁场中运动的轨道半径R;
(2)粒子从M点运动到P点的总时间 ;
;
(3)匀强电场的场强大小E。
一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s后警车发动起来,并以2.5m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h以内。问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
“∟”形轻杆两边互相垂直、长度均为l,可绕过O点的水平轴在竖直平面内自由转动。两端各固定一个金属小球A、B;其中A球质量为m、带负电、电荷量为q(q > 0);B球不带电,质量为 m。重力加速度为g 。现将“∟”形杆从OB位于水平位置由静止释放。已知sin37°=0.6,cos37°=0.8。求:
m。重力加速度为g 。现将“∟”形杆从OB位于水平位置由静止释放。已知sin37°=0.6,cos37°=0.8。求:
(1)A、B两球的最大动能之和为多少?
(2)若在空间加竖直向下的匀强电场,OB杆仍从原来位置释放后,能转过的最大角度为127°,则该电场的电场强度大小为多少?
如图所示,两根质量均为m、电阻均为R、长度均为l的导体棒a、b,用两条等长的、质量和电阻均可忽略的、不可伸长的柔软长直导线连接后,b放在距地面足够高的光滑绝缘水平桌面上,a靠在桌子的光滑绝缘侧面上;两根导体棒均与桌子边缘平行。整个空间存在水平向右的匀强磁场,磁感应强度为B。开始时两棒静止,自由释放后开始运动,导体棒a在落地前就已匀速运动,此时导体棒b仍未离开桌面。已知两条导线除桌边拐弯处外其余部位均处于伸直状态,导线与桌子侧棱间无摩擦。
(1)试求导体棒匀速运动时的速度大小。
(2)从自由释放到刚匀速运动的过程中,若通过导体棒横截面的电荷量为q,求该过程中系统产生的焦耳热。
如图所示,在平面直角坐标系xOy中,第Ⅰ象限内有平行于 轴的匀强电场,方向沿y轴正方向;第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里。正三角形边长为L,且
轴的匀强电场,方向沿y轴正方向;第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里。正三角形边长为L,且 边与y轴平行。质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力。试求:
边与y轴平行。质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力。试求:
(1)电场强度的大小。
(2)粒子到达a点时速度的大小和方向。
(3)△abc区域内磁场的磁感应强度的最小值。
如图所示,质量M = 4.0kg的木板长L =" 2.0" m,静止在水平地面上,木板与地面间的动摩擦因数为μ1=0.05。木板水平上表面左端静置质量m =" 2.0" kg的小滑块(可视为质点),小滑块与板间的动摩擦因数为μ2 = 0.2。从某时刻开始,用F="5.0" N的水平力一直向右拉滑块,直至滑块滑离木板。设木板与地面间的最大静摩擦力等于滑动摩擦力,取g ="10" m/s2。试求:
(1)此过程中木板的位移大小。
(2)滑块离开木板时的速度大小。
如图所示,在xoy坐标系第一象限内有匀强磁场,磁场区域上边界刚好与直线y=a重合,磁感应强度为B。一个带正电的离子在坐标为(a,0)的A点以某一速度进入磁场区域,进入磁场时速度方向与x轴正向夹角为30°,离子质量为m,带电量为q。不计离子重力。
(1)若离子离开磁场时位置坐标为(a,a )的C点,求离子运动的速度大小?
(2)当离子进入磁场的速度满足什么条件时可使离子在磁场区域运动的时间最长?并求出最长时间是多少?
如图所示,在竖直平面内建立xOy直角坐标系,Oy表示竖直向上的方向。已知该平面内存在沿x轴负方向的区域足够大的匀强电场,现有一个带电量为2.5×10-4C,质量为0.5kg 的小球从坐标原点O沿y轴正方向以一定的初速度竖直向上抛出,它到达的最高点位置为图中的Q点,不计空气阻力,g取10 m/s2。试分析求解:
(1) 小球带何种电荷;
(2) 该匀强电场的电场强度大小;
(3) 小球从O点抛出到落回x轴的过程中电势能的改变量;
(4) 小球落回x轴时的动能。
有一平行板电容器,内部为真空,两个极板的间距为 ,极板长为L,极板间有一匀强电场,U为两极板间的电压,电子从极板左端的正中央以初速
,极板长为L,极板间有一匀强电场,U为两极板间的电压,电子从极板左端的正中央以初速 射入,其方向平行于极板,并打在极板上的D点,如图所示。电子的电荷量用e表示,质量用
射入,其方向平行于极板,并打在极板上的D点,如图所示。电子的电荷量用e表示,质量用 表示,重力不计。求
表示,重力不计。求
(1)电子打到D点时的动能;
(2)D点与电子出发点间的水平距离;
(3)电子的初速必须满足什么条件,电子才能飞出极板。
如图所示,两个平行金属板AB中间为一匀强电场,AB相距10cm,CD为电场中的两点,CD=8cm,CD连线和电场方向成60°角,C点到A板的距离为2cm。已知质子从C点移到D点,电场力作功为3.2×10-17J。(质子带电量为1.6×10-19C)求:
(1)匀强电场的电场强度;
(2)AB两板之间的电势差;
(3)若将A板接地,则C、D两点的电势各为多大?
重为G=0.1N的金属棒ab,放在光滑的平行金属导轨上,如图所示,轨道间距为L=0.5m,所在平面与水平面的夹角为30º,匀强磁场垂直于轨道平面向上,电源电动势E=3V,金属棒电阻R=6Ω,其余电阻不计,若金属棒恰好静止,求:

(1)金属棒所受安培力的方向;
(2)磁感应强度的大小。
试题篮
()