用1,2,3,4,5,6,7这7个数字组成3个两位数,1个一位数,并且使这4个数的和等于100.我们要求最大的两位数尽可能小,那么这个最大的两位数是多少?
(5○13○7)○(17○9)=12。
把+,一,×,÷这4个运算符号,分别填入上面等式的圆圈内,使等式成立。
计算:1000+999—998—997+996+995—994—993+…+108+107-106-105+104+103-102-101.
在10,9,8,7,6,5,4,3,2,1这10个数的每相邻两个数之间都填上一个加号或一个减号,组成一个算式。要求同时满足以下条件:
①算式的结果等于37,
②这个算式的所有减数(即前面填了减号的数)的乘积尽可能地大。
那么这些减数的最大乘积是多少?
你能利用规律直接写一写吗?
1+3+5+7=4²=16 1+3+5+7+9=5²=25 1+3+5+7+9+11=6²=36
求:1+3+5+7+9+11+13+15+17=( ) 1+3+5+7+5+3+1 =( )
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
利用公式1×1+2×2+…+n×n=n×(n+1)×(2×n+1)÷6,计算:15×15+16×16+…+21×21.
计算:(1998+19981998+199819981998+…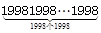 )÷(1999+19991999+199919991999…
)÷(1999+19991999+199919991999… 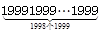 )×1999
)×1999
我们把相差为2的两个奇数称为连续奇数.已知自然数1111155555是两个连续奇数的乘积,那么这两个奇数的和是多少?
试题篮
()