小学数学整除性质解答题

在1994的右边补上三个数字，变成一个七位数M．若M能被3、4、5整除，求M的最大值．

学校买来65个球，如果每3个装一盒，能正好装完吗？如果每5个装一盒，能正好装完吗？

把若干个自然数l，2，3，…乘到一起，如果已知这个乘积的最末十三位恰好都是零，那么最后出现的自然数最小应该是多少?

有一个6位数112AA4能被9整除，求A．

一个三位数能被9整除，去掉它的末位数后，所得的两位数是17的倍数。这样的三位数中，最大是几？

修改31743的某一个数字，可以得到823的倍数．问修改后的这个数是多少?

如图，依次排列的5个数是13，12，15，25，20．它们每相邻的两个数相乘得4个数．这4个数每相邻的两个数相乘得3个数．这3个数每相邻的两个数相乘得2个数．这2个数相乘得1个数．请问：最后这个数从个位起向左数，可以连续地数出几个零?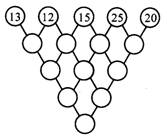

从0，1，2，3，4，5，6，7，8，9这10个数字中选出5个不同的数字组成一个五位数，使它能被3，5，7，13整除，这个数最大是多少?

以多位数为例，说明被7、11、13整除的规律.

已知九位数既是9的倍数，又是11的倍数；那么，这个九位数是多少？

有三个连续自然数，其中最小的能被15整除，中间的能被17整除，最大的能被19整除，请写出一组这样的三个连续自然数．

如果六位数1992□□能被105整除，那么它的最后两位数是多少?

六位数能被99整除，是多少？

试说明一个4位数，原序数与反序数的和一定是11的倍数(如：1236为原序数，那么它对应的反序数为6321，它们的和7557是11的倍数．)

（吴中区）有一个六位数，它的二倍、三倍、四倍、五倍、六倍还是六位数，并且它们的数字和原来的六位数的数字完全相同只是排列的顺序不一样，求这个六位数．