初中数学试题

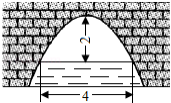
如图，一抛物线型拱桥，当拱顶到水面的距离为2米时，水面宽度为4米；那么当水位下降1米后，水面的宽度为　     　米．

关于 $x$的方程 $2x^2-\mathit{ax}+1=0$一个根是1，则它的另一个根为　     　．

一个整数的所有正约数之和可以按如下方法求得，如：

$6=2\times 3$，则6的所有正约数之和 $(1+3)+(2+6)=(1+2)\times (1+3)=12$；

$12=2^2\times 3$，则12的所有正约数之和 $(1+3)+(2+6)+(4+12)=(1+2+2^2)\times (1+3)=28$；

$36=2^2\times 3^2$，则36的所有正约数之和

$(1+3+9)+(2+6+18)+(4+12+36)=(1+2+2^2)\times (1+3+3^2)=91$．

参照上述方法，那么200的所有正约数之和为 $($　　 $)$

A．420B．434C．450D．465

如图是二次函数 $y=a{x}^2+\mathit{bx}+c$的图象，其对称轴为 $x=1$，下列结论：① $\mathit{abc}>0$；② $2a+b=0$；③ $4a+2b+c<0$；④若 $(-\frac{3}{2},y_1)$， $(\frac{10}{3},y_2)$是抛物线上两点，则 $y_1<y_2$其中结论正确的是 $($　　 $)$

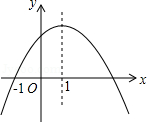
A．①②B．②③C．②④D．①③④

如图， $P$为平行四边形 $\mathit{ABCD}$边 $\mathit{AD}$上一点， $E$、 $F$分别是 $\mathit{PB}$、 $\mathit{PC}$（靠近点 $P)$的三等分点， $\mathit{\Delta PEF}$、 $\mathit{\Delta PDC}$、 $\mathit{\Delta PAB}$的面积分别为 $S_1$、 $S_2$、 $S_3$，若 $\mathit{AD}=2$， $\mathit{AB}=2\sqrt{3}$， $\angle A=60°$，则 $S_1+S_2+S_3$的值为 $($　　 $)$

A． $\frac{10}{3}$B． $\frac{9}{2}$C． $\frac{13}{3}$D．4

下列命题：①若 $a<1$，则 $(a-1)\sqrt{\frac{1}{1-a}}=-\sqrt{1-a}$；②平行四边形既是中心对称图形又是轴对称图形；③ $\sqrt{9}$的算术平方根是3；④如果方程 $a{x}^2+2x+1=0$有两个不相等的实数根，则实数 $a<1$．其中正确的命题个数是 $($　　 $)$

A．1个B．2个C．3个D．4个

2015年某县 $\mathit{GDP}$总量为1000亿元，计划到2017年全县 $\mathit{GDP}$总量实现1210亿元的目标．如果每年的平均增长率相同，那么该县这两年 $\mathit{GDP}$总量的平均增长率为 $($　　 $)$

A． $1.21\%$B． $8\%$C． $10\%$D． $12.1\%$

积极行动起来，共建节约型社会！我市某居民小区200户居民参加了节水行动，现统计了10户家庭一个月的节水情况，将有关数据整理如下：

节水量（单位：吨）	0.5	1	1.5	2
家庭数（户）	2	3	4	1

请你估计该200户家庭这个月节约用水的总量是 $($　　 $)$

A．240吨B．360吨C．180吨D．200吨

正比例函数 $y_1=k_{1}x(k_1>0)$与反比例函数 $y_2=\frac{k_2}{x}(k_2>0)$部分图象如图所示，则不等式 $k_{1}x>\frac{k_2}{x}$的解集在数轴上表示正确的是 $($　　 $)$

A．B．

C．D．

每到四月，许多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其扰，据测定，杨絮纤维的直径约为 $0.0000105m$，该数值用科学记数法表示为 $($　　 $)$

A． $1.05\times {10}^5$B． $0.105\times {10}^{-4}$C． $1.05\times {10}^{-5}$D． $105\times {10}^{-7}$

小红把一把直尺与一块三角板如图放置，测得 $\angle 1=48°$，则 $\angle 2$的度数为 $($　　 $)$

A． $38°$B． $42°$C． $48°$D． $52°$

下列各式的运算正确的是 $($　　 $)$

A． $\frac{a^3}{a}=a$B． $a^2+a=2a^3$C． ${(-2a)}^2=-2a^2$D． ${\left(a^3\right)}^2=a^6$

如图，小明同学将一个圆锥和一个三棱柱组成组合图形，观察其三视图，其俯视图是 $($　　 $)$

A．B．

C．D．

以下选项中比 $|-\frac{1}{2}|$小的数是 $($　　 $)$

A．1B．2C． $\frac{1}{2}$D． $-\frac{1}{2}$

问题提出：如何将边长为 $n(n⩾5$，且 $n$为整数）的正方形分割为一些 $1x5$或 $2\times 3$的矩形（ $\mathit{axb}$的矩形指边长分别为 $a$， $b$的矩形）？

问题探究：我们先从简单的问题开始研究解决，再把复杂问题转化为已解决的问题．

探究一：

如图①，当 $n=5$时，可将正方形分割为五个 $1\times 5$的矩形．

如图②，当 $n=6$时，可将正方形分割为六个 $2\times 3$的矩形．

如图③，当 $n=7$时，可将正方形分割为五个 $1\times 5$的矩形和四个 $2\times 3$的矩形

如图④，当 $n=8$时，可将正方形分割为八个 $1\times 5$的矩形和四个 $2\times 3$的矩形

如图⑤，当 $n=9$时，可将正方形分割为九个 $1\times 5$的矩形和六个 $2\times 3$的矩形

探究二：

当 $n=10$，11，12，13，14时，分别将正方形按下列方式分割：

所以，当 $n=10$，11，12，13，14时，均可将正方形分割为一个 $5\times 5$的正方形、一个 $(n-5)\times (n-5)$的正方形和两个 $5\times (n-5)$的矩形．显然， $5\times 5$的正方形和 $5\times (n-5)$的矩形均可分割为 $1\times 5$的矩形，而 $(n-5)\times (n-5)$的正方形是边长分别为5，6，7，8，9的正方形，用探究一的方法可分割为一些 $1\times 5$或 $2\times 3$的矩形．

探究三：

当 $n=15$，16，17，18，19时，分别将正方形按下列方式分割：

请按照上面的方法，分别画出边长为18，19的正方形分割示意图．

所以，当 $n=15$，16，17，18，19时，均可将正方形分割为一个 $10\times 10$的正方形、一个 $(n-10)\times (n-10)$的正方形和两个 $10\times (n-10)$的矩形．显然， $10\times 10$的正方形和 $10\times (n-10)$的矩形均可分割为 $1x5$的矩形，而 $(n-10)\times (n-10)$的正方形又是边长分别为5，6，7，8，9的正方形，用探究一的方法可分割为一些 $1\times 5$或 $2\times 3$的矩形．

问题解决：如何将边长为 $n(n⩾5$，且 $n$为整数）的正方形分割为一些 $1\times 5$或 $2\times 3$的矩形？请按照上面的方法画出分割示意图，并加以说明．

实际应用：如何将边长为61的正方形分割为一些 $1\times 5$或 $2\times 3$的矩形？（只需按照探究三的方法画出分割示意图即可）