初中数学试题

如图，在平行四边形ABCD中，AD=5cm，AP=8cm，AP平分∠DAB，交DC于点P，过点B作BE⊥AD于点E，BE交AP于点F，则tan∠BFP=      ．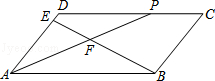

如图所示，已知抛物线y=x²﹣1与x轴交于A、B两点，与y轴交于点C．

（1）求A、B、C三点的坐标；
（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积；
（3）在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似？若存在，请求出M点的坐标；否则，请说明理由．

已知二次函数y=﹣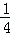x²+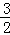x的图象如图．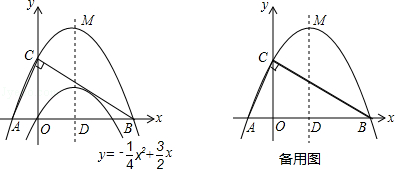

（1）求它的对称轴与x轴交点D的坐标；
（2）将该抛物线沿它的对称轴向上平移，设平移后的抛物线与x轴，y轴的交点分别为A、B、C三点，若∠ACB=90°，求此时抛物线的解析式．

两个反比例函数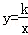和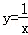在第一象限内的图象如图所示，点P在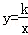的图象上，PC⊥x轴于点C，交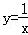的图象于点A，PD⊥y轴于点D，交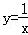的图象于点B，当点P在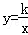的图象上运动时，以下结论：
①△ODB与△OCA的面积相等；②四边形PAOB的面积不会发生变化；③PA与PB始终相等；④当点A是PC的中点时，点B一定是PD的中点．
其中一定正确的是      （把你认为正确结论的序号都填上）．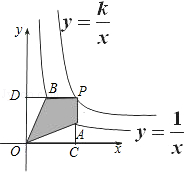

如图1，已知二次函数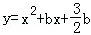的图象与x轴交于A、B两点（B在A的左侧），顶点为C，点D（1，m）在此二次函数图象的对称轴上，过点D作y轴的垂线，交对称轴右侧的抛物线于E点．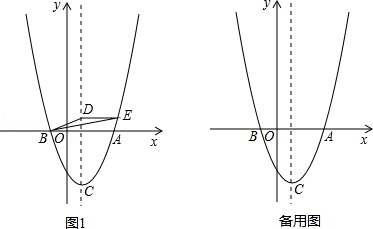

（1）求此二次函数的解析式和点C的坐标；
（2）当点D的坐标为（1，1）时，连接BD、BE．求证：BE平分∠ABD；
（3）点G在抛物线的对称轴上且位于第一象限，若以A、C、G为顶点的三角形与以G、D、E为顶点的三角形相似，求点E的横坐标．

已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE．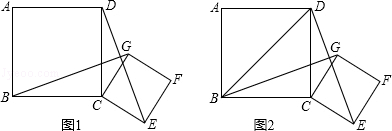

（1）如图1，连接BG、DE．求证：BG=DE；
（2）如图2，如果正方形ABCD的边长为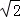，将正方形CEFG绕着点C旋转到某一位置时恰好使得CG∥BD，BG=BD．
①求∠BDE的度数；
②请直接写出正方形CEFG的边长的值．

二次函数y=x²﹣8x+15的图象与x轴相交于A、B两点，P点在该函数图象上运动，能使△ABP的面积为1的点P有      个．

定义：把一个半圆与抛物线的一部分合成封闭图形，我们把这个封闭图形称为“蛋圆”．如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，A，B，C，D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0，8），AB为半圆的直径，半圆的圆心M的坐标为（1，0），半圆半径为3．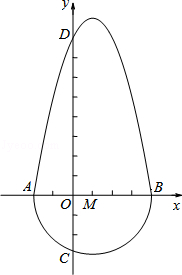

（1）请你直接写出“蛋圆”抛物线部分的解析式y     ，自变量的取值范围是     ；
（2）请你求出过点C的“蛋圆”切线与x轴的交点坐标；
（3）求经过点D的“蛋圆”切线的解析式．

（1）在Rt△ABC中，∠C=90°，∠B=30°．

①△ABC绕点C顺时针旋转得到△DEC，点D恰好落在AB边上．如图1，则S_△BDC与S_△AEC的数量关系是     ；
②当△DEC绕点C旋转到图2的位置时，小娜猜想①中S_△BDC与S_△AEC的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明小娜的猜想；
（2）已知，∠ABC=60°，点D是∠ABC平分线上一点，BD=CD=2，DE∥AB交BC于点E，如图3．若在射线BA上存在点F，使S_△DCF=S_△BDE，则BF=     ．

已知AB是圆O的直径，D是AB延长线上一点，DC是圆O的切线，C是切点，连结AC，若∠CAB=30°，则∠ADC=      ．

(6分)如图，△ABC中，AB=AC，∠BAC=45°，BD⊥AC，垂足为D点，AE平分∠BAC，交BD于F，交BC于E，点G为AB的中点，连接DG，交AE于点H，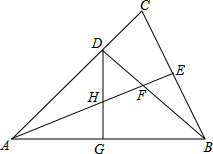

（1）求∠ACB的度数；
（2）HE=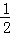AF．

已知在△ABC中，CD是∠ACB的平分线，∠A=2∠B，AD=3，AC=5，则BC=     ．

如图所示，在等边三角形ABC中，O是三个内角平分线的交点，OD∥AB，OE∥AC，则图中等腰三角形的个数是（ ）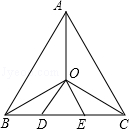

A．7

B．6

C．5

D．4

如图，在△ABC中，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F，请你判断并写出FE与FD之间的数量关系；请说明理由．

如图，在△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，那么∠C=  度．