初中数学试题

（本题满分 10分）如图是一个“数值转换机”（箭头是指数进入转换机的路径,方框是对进入的数进行转换的转换机）。

（1）当小明输入4, 7, - ,-2012 这四个数使,则四次输出的结果依次为        ,        ,        ,        。
（2）你认为当输入数 等于             时（写出一个即可）,其输出结果为0。
（3）你认为这个“数值转换机”不可能输出        数。
（4）有一次,小明在操作的时候,输出的结果是2,聪明的你判断一下,小明输入的正整数是        （用含自然数n的代数式表示）。

某同学在A、B两家超市发现他看中的随身听的单价相同，书包单价也相同，随身听和书包单价之和是452元，且随身听的单价比书包单价的4倍少8元．
（1）求该同学看中的随身听和书包单价各是多少元？
（2）某一天该同学上街，恰好赶上商家促销，超市A所有商品打八折销售，超市B全场购物满100元返购物券30元销售（不足100元不返券，购物券全场通用），该同学只带了400元钱，他能否在这两家超市都可以买下看中的这两样商品？若两家都可以选择，在哪一家购买更省钱？

如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，…，按此规律．则第（n）个图形中面积为1的正方形的个数为         .

（本题10分）司机在驾驶汽车时，发现紧急情况到踩下刹车需要一段时间，这段时间叫反应时间，之后还会继续行驶一段距离．我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”（如图）．

已知汽车的刹车距离（单位：米）与车速（单位：米/秒）之间有如下关系：，其中为司机的反应时间（单位：秒），为制动系数．某机构为测试司机饮酒后刹车距离的变化，对某种型号的汽车进行了“醉汉”驾车测试，已知该型号汽车的制动系数，并测得志愿者在未饮酒时的反应时间秒．
（1）若志愿者未饮酒，且车速为10米/秒，则该汽车的刹车距离为        米 ；
（2）当志愿者在喝下一瓶啤酒半小时后，以15米/秒的速度驾车行驶，测得刹车距离为52.5米，此时该志愿者的反应时间是        秒．
（3）假如该志愿者当初是以10米/秒的车速行驶，则刹车距离将比未饮酒时增加多少？

已知，求代数式
的值.

长为1，宽为的长方形纸片（），如图那样折一下，剪下一个边长等于长方形的宽度的正方形（称为第一次操作）；再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n次操作后，剩下的图形为正方形，则操作终止．当n=3时，的值为­­­­________．

观察下列各式：



（1）计算：的值；
（2）计算：的值；
（3）猜想：的值。

如图，AB∥EF，∠C，则、、的关系是______________．

a为有理数，定义运算符号“※”：当a＞－2时，※a＝－a；当a＜－2时，※a＝a；当a＝－2时，※a＝0．根据这种运算，则※[4＋※（2－5）]的值为（    ）

A．1

B．－1

C．7

D．－7

（本小题满分12分）在“五一”黄金周期间，小明、小亮等同学随家人一同到江郎山游玩，看见门口有如下票价提示：“成人：35元/张；学生：按成人票5折优惠；团体票（16人以上含16人）：按成人票价六折优惠”。
在购买门票时，小明与他爸爸有如下对话，爸爸：“大人门票每张35元，学生门票对折优惠，我们共有12人，共需350元”。小明：“爸爸，等一下，让我算一算，换一种方式买票是不是可以更省钱”。
问题：（1）小明他们一共去了几个成人，几个学生？
（2）请你帮小明算一算，用哪种方式买票更省钱？说明理由

如图，半径为1个单位的圆片上有一点Q与数轴上的原点重合（提示:圆的周长C=2r）

（1）把圆片沿数轴向左滚动1周，点Q到达数轴上点A的位置，点A表示的数是_________；
（2）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录
如下：+2, -1, -5, +4, +3, -2
①第几次滚动后,Q点距离原点最近？第几次滚动后,Q点距离原点最远？
②当圆片结束运动时，Q点运动的路程共有多少?此时点Q所表示的数是多少?

在平面直角坐标系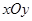中，点M（，），以点M为圆心，OM长为半径作⊙M ，使⊙M与直线OM的另一交点为点B，与x轴、y轴的另一交点分别为点D，A（如图），连接AM点P是弧AB上的动点.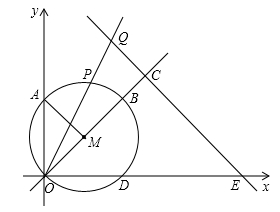

（1）写出∠AMB的度数；
（2）点Q在射线OP上，且OP·OQ=20，过点Q作QC垂直于直线OM，垂足为C，直线QC交x轴于点E.
①当动点P与点B重合时，求点E的坐标；
②连接QD，设点Q的纵坐标为t，△QOD的面积为S，求S与t的函数关系式及S的取值范围.

如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若DE=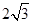，∠DPA=45°．

（1）求⊙O的半径；
（2）求图中阴影部分的面积.

如图，已知抛物线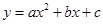 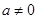（）的顶点坐标为（4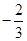，），且与y轴交于点C（0，2），与x轴交于A、B两点（点A在点B的左边）.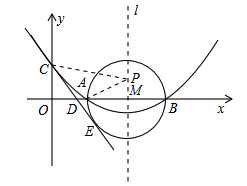

（1）求抛物线的解析式及A、B两点的坐标；
（2）在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小，若存在，求AP+CP的最小值；若不存在，请说明理由；
（3）在以AB为直径的⊙M中，CE与⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．

如图，在平面直角坐标系xOy中，直线y=x+4与坐标轴分别交于A、B两点，过A、B两点的抛物线为y=－x²+bx+c．点D为线段AB上一动点，过点D作CD⊥x轴于点C，交抛物线于点E．

（1）求抛物线的解析式．
（2）当DE=4时，求四边形CAEB的面积．
（3）连接BE，是否存在点D，使得△DBE和△DAC相似？若存在，直接写出点D坐标；若不存在，说明理由．