已知二次函数 .
(1)若 ,且该二次函数的图象过点 ,求c的值;
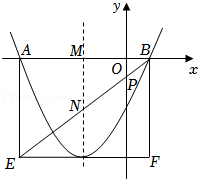
(2)如图所示,在平面直角坐标系xOy中,该二次函数的图象与x轴相交于不同的两点 、 ,其中 、 ,且该二次函数的图象的顶点在矩形 的边 上,其对称轴与 轴、 分别交于点 与 轴相交于点 ,且满足 .
①求关于 的一元二次方程 的根的判别式的值;
②若 ,令 ,求 的最小值.
阅读材料:十六世纪的法国数学家弗朗索瓦•韦达发现了一元二次方程的根与系数之间的关系,可表述为“当判别式 时,关于 的一元二次方程 的两个根 有如下关系: , ”.此关系通常被称为“韦达定理”.
如图所示, 的顶点 在 上,顶点 在 外,边 与 相交于点 , ,连接 ,已知 .
(1)求证:直线 是 的切线;
(2)若线段 与线段 相交于点 ,连接 .
①求证: ;
②若 ,求 的半径的长度.

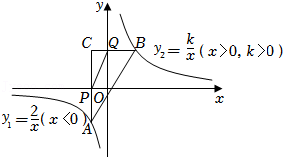
如图所示,在平面直角坐标系 中,点 分别在函数 、 的图象上,点 在第二象限内, 轴于点 , 轴于点 ,连接 ,已知点 的纵坐标为 .
(1)求点 的横坐标;
(2)记四边形 的面积为 ,若点 的横坐标为 ,试用含 的代数式表示 .
如图,在平面直角坐标系中,矩形 的顶点 , 在 轴的正半轴上,反比例函数 的图象经过顶点 ,分别与对角线 ,边 交于点 , ,连接 , .若点 为 的中点, 的面积为1,则 的值为

| A. |
|
B. |
|
C. |
2 |
D. |
3 |
关于 的分式方程 的解为正数,且使关于 的一元一次不等式组 有解,则所有满足条件的整数 的值之和是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系中,菱形 的顶点 在第二象限,其余顶点都在第一象限, 轴, , .过点 作 ,垂足为 , .反比例函数 的图象经过点 ,与边 交于点 ,连接 , , .若 ,则 的值为

| A. |
|
B. |
|
C. |
7 |
D. |
|
若关于 的一元一次不等式组 的解集为 ,且关于 的分式方程 的解是正整数,则所有满足条件的整数 的值之和是
| A. |
5 |
B. |
8 |
C. |
12 |
D. |
15 |
如图,相邻两个山坡上,分别有垂直于水平面的通信基站 和 .甲在山脚点 处测得通信基站顶端 的仰角为 ,测得点 距离通信基站 的水平距离 为 ;乙在另一座山脚点 处测得点 距离通信基站 的水平距离 为 ,测得山坡 的坡度 .若 ,点 , , , 在同一水平线上,则两个通信基站顶端 与顶端 的高度差为(参考数据: ,

| A. |
|
B. |
|
C. |
|
D. |
|
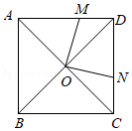
如图,正方形 的对角线 , 交于点 , 是边 上一点,连接 ,过点 作 ,交 于点 .若四边形 的面积是1,则 的长为
| A. |
1 |
B. |
|
C. |
2 |
D. |
|
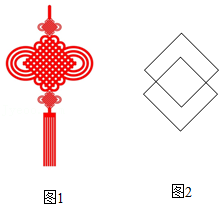
数学兴趣小组同学从"中国结"的图案(图 中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是
| A. |
用3个相同的菱形放置,最多能得到6个菱形 |
| B. |
用4个相同的菱形放置,最多能得到16个菱形 |
| C. |
用5个相同的菱形放置,最多能得到27个菱形 |
| D. |
用6个相同的菱形放置,最多能得到41个菱形 |
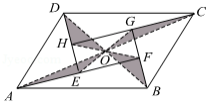
如图是一个由5张纸片拼成的平行四边形 ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 ,另两张直角三角形纸片的面积都为 ,中间一张矩形纸片 的面积为 , 与 相交于点 .当 , , , 的面积相等时,下列结论一定成立的是
| A. |
|
B. |
|
C. |
|
D. |
|
已知抛物线 与 轴的交点为 和 ,点 , , , 是抛物线上不同于 , 的两个点,记△ 的面积为 ,△ 的面积为 ,有下列结论:①当 时, ;②当 时, ;③当 时, ;④当 时, .其中正确结论的个数是
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
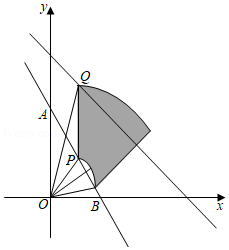
如图,直线 与坐标轴交于 、 两点,点 是线段 上的一个动点,过点 作 轴的平行线交直线 于点 , 绕点 顺时针旋转 ,边 扫过区域(阴影部分)面积的最大值是
| A. |
|
B. |
|
C. |
|
D. |
|
在 中, ,分别过点 , 作 平分线的垂线,垂足分别为点 , , 的中点是 ,连接 , , .则下列结论错误的是
| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()