一辆公共汽车从起点站开出后,途中经过6个停靠站,最后到达终点站。下表记录了这辆公共汽车全程载客变化情况。
| 停靠站 |
起点站 |
中间 第1站 |
中间 第2站 |
中间 第3站 |
中间 第4站 |
中间 第5站 |
中间 第6站 |
终点站 |
| 上下车人数 |
+21 |
-3 +8 |
-4 +2 |
0 +4 |
-7 +1 |
-9 +6 |
-7 0 |
-12 |
(1)中间第4站上车人数是人_________,下车人数是人_________;
(2)中间的6个站中,第_________站没有人上车,第_________站没有人下车;
(3)中间第二站开车时车上人数是_______人,第五站停车时车上人数是_________人;
(4)从表中你还能知道的一个信息是_________
已知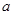 、
、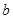 互为相反数且
互为相反数且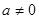 ,
, 、
、 互为倒数,
互为倒数,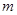 的绝对值是最小的正整数,
的绝对值是最小的正整数,
求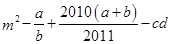 的值. (注:
的值. (注: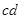 =
=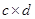 )
)
解:∵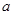 、
、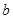 互为相反数且
互为相反数且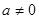 , ∴
, ∴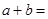 __________,
__________, __________;
__________;
又∵ 、
、 互为倒数,∴
互为倒数,∴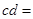 __________;
__________;
又∵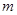 的绝对值是最小的正整数, ∴
的绝对值是最小的正整数, ∴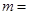 __________,∴
__________,∴ __________;
__________;
∴原式 __________.
__________.
某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下(单位:千米):
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
| -3 |
+8 |
-9 |
+10 |
+4 |
-6 |
-2 |
(1)在第几次行驶时距A地最远?
(2)收工时距A地多远?
(3)若每千米耗油0.3升,每升汽油需7.2元,问检修小组工作一天需汽油费多少元?
观察下列等式
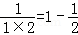 ,
,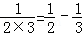 ,
,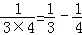 ,
,
将以上三个等式两边分别相加得:
 =1﹣
=1﹣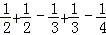 =1﹣
=1﹣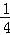 =
= .
.
(1)猜想并写出: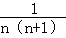 .
.
(2)根据以上规律直接写出下列各式的计算结果:
①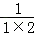 +
+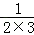 +
+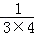 +…+
+…+ = ;
= ;
②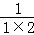 +
+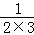 +
+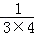 +…+
+…+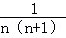 .
.
(3)探究并计算: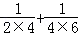 +
+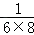 +…+
+…+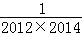 .
.
观察下列各式:
﹣1× =﹣1+
=﹣1+
﹣ ×
× =﹣
=﹣ +
+
﹣ ×
×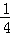 =﹣
=﹣ +
+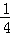
…
(1)你能探索出什么规律?(用文字或表达式)
(2)试运用你发现的规律计算:
(﹣1× )+(﹣
)+(﹣ ×
× )+(﹣
)+(﹣ ×
×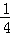 )+…+(﹣
)+…+(﹣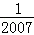 ×
×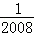 )+(﹣
)+(﹣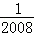 ×
×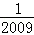 )
)
10名学生体检测体重,以50千克为基准,超过的数记为正,不足的数记为负,称得结果如下(单位:千克)
2,3,﹣7.5,﹣3,5,﹣8,3.5,4.5,8,﹣1.5.这10名学生的总体重为多少?平均体重为多少?
一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升?
观察下列各式:
13+23= ;
;
13+23+33=36= ;
;
13+23+33+43=100= ;
;
(1)计算:13+23+33+43+53的值;
(2)计算:13+23+33+43+…+103的值;
(3)猜想:13+23+33+43+…+n3的值.
图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n= .
.

如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
试题篮
()