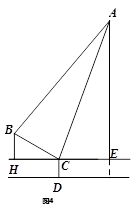
(本题8分)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°。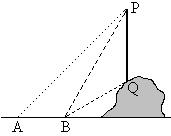
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m)。备用数据: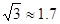 ,
,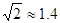
如图3图4,分别是吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A点距地面的高度是多少米?(精确到0.1米)?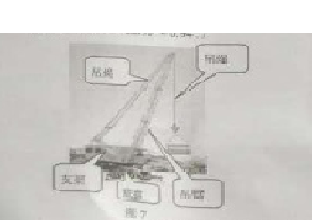
(参考数据:sin10°=cos80°=0.17,cos10°=sin80°=0.98,sin20°=cos70°=0.34,tan70°=2.75,sin70°=0.94)
定义:如图1,平面上两条直线AB、CD相交于点O,对于平面内任意一点M,点M到直线AB、CD的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”为(0,0)点有1个,即点O.
(1)“距离坐标”为(1,0)点有 个;
(2)如图2,若点M在过点O且与直线CD垂直的直线l上时,点M的“距离坐标”为(p,q),且∠BOD=120°.请画出图形,并直接写出p,q的关系式;
(3)如图3,点M的“距离坐标”为(1,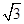 ),且∠AOB=30°,求OM的长.
),且∠AOB=30°,求OM的长.
如图所示,体育场内一看台与地面所成夹角为
,看台最低点A到最高点B的距离为
,
,
两点正前方有垂直于地面的旗杆
.在
,
两点处用仪器测量旗杆顶端
的仰角分别为
和
(仰角即视线与水平线的夹角)
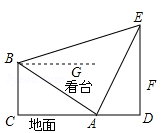
(1)求
的长;
(2)已知旗杆上有一面旗在离地1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(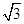 =1.7).
=1.7).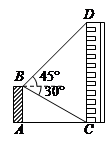
某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).
(本题10分)如图,某校综合实践活动小组的同学欲测量公园内一棵树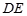 的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端
的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端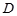 的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端
的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端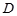 的仰角为60°.已知点A 的高度AB为
的仰角为60°.已知点A 的高度AB为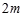 ,台阶AC的坡度为
,台阶AC的坡度为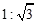 (即
(即 ),且
),且 、
、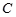 、
、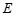 三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65°
三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65° 2.1,cos65°
2.1,cos65° 0.4, sin35°
0.4, sin35° 0.6,tan35°
0.6,tan35° 0.7,
0.7, 1.7,结果保留一位小数).
1.7,结果保留一位小数).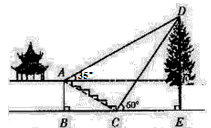
如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
(1)若点M的坐标为(3,4),
①求A,B两点的坐标;
②求ME的长.
(2)若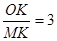 ,求∠OBA的度数.
,求∠OBA的度数.
(3)设tan∠OBA=x(0<x<1),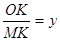 ,直接写出y关于x的函数解析式.
,直接写出y关于x的函数解析式.
(本小题满分6分)小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°和35°,已知大桥BC与地面在同一水平面上,其长度为100m。请求出热气球离地面的高度。(结果保留整数,参考数据: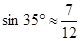 ,
,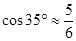 ,
,

2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.
(1)求∠DAC的度数;
(2)求这棵大树原来的高度是多少米?(结果精确到个位,参考数据: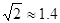 ,
, ,
,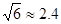 )
)
如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度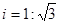 ,AB=10米,AE=15米.
,AB=10米,AE=15米.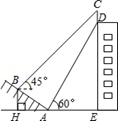
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: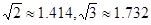 )
)
如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.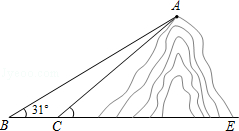
(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31°≈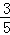 ,sin31°≈
,sin31°≈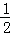 ,tan39°≈
,tan39°≈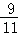 ,sin39°≈
,sin39°≈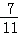 )
)
如图,在△ABC中,AB=AC=1,点D,E在直线BC上运动.设BD=x,CE=y.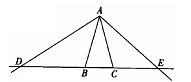
(l)如果∠BAC=300,∠DAE=l050,试确定y与x之间的函数关系式;
(2)如果∠BAC=α,∠DAE=β,当α,β满足怎样的关系时,(l)中y与x之间的函数关系式还成立?试说明理由.
如图,小红站在水平面上的点A处,测得旗杆BC顶点C的仰角为60°,点A到旗杆的水平距离为a米.若小红的水平视线与地面的距离为b米,则旗杆BC的长为________米。(用含有a、b的式子表示)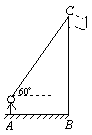
试题篮
()