初中数学计算器—基础知识解答题

小丽驾车从甲地到乙地。设她出发第x min时的速度为y km/h，图中的折线表示她在整个驾车过程中y与x之间的函数关系。

（1）小丽驾车的最高速度是        km/h；
（2）当20£x£30时，求y与x之间的函数关系式，并求出小丽出发第22 min时的速度；
（3）如果汽车每行驶100 km耗油10 L，那么小丽驾车从甲地到乙地共耗油多少升？

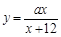通常儿童服药量要少于成人．某药厂用来计算儿童服药量的公式为，其中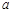为成人服药量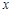，为儿童的年龄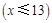．问：
（1）3岁儿童服药量占成人服药量的          ；
（2）请求出哪个年龄的儿童服药量占成人服药量的一半？

国际象棋中的“皇后”不仅能控制她所在的行与列的每一个小方格，而且还能控制“斜”方向的两条直线上的每个小方格，如图甲所示.
（1）在图乙小方格中有一“皇后Q”他所在的位置可用（2，3）来表示，请说明“皇后Q”所在的位置（2，3）的意义，并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置；
（2）图丙是一个4×4的小方格棋盘，请在这个棋盘中放入四个“皇后Q”，使这四个“皇后Q”之间胡不受对方控制.（在图丙中标出字母Q即可）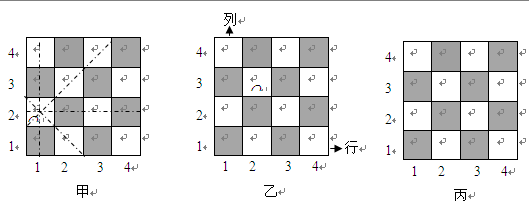

正方形边长为3，若边长增加则面积增加，求随变化的函数关系式，并以表格的形式表示当等于1、2、3、4时的值．

如图，在平面直角坐标系中，函数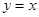的图象是第一、三象限的角平分线．
实验与探究：由图观察易知A（0，2）关于直线的对称点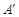的坐标为（2，0），请在图中分别标明B(5,3) 、C(-2,5) 关于直线的对称点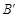、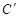的位置，并写出它们的坐标:              、          ；
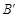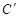归纳与发现：结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(m,n)关于第一、三象限的角平分线的对称点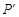的坐标为           ；
运用与拓广：已知两点D(0,-3)、E(-1,-4)，试在直线上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．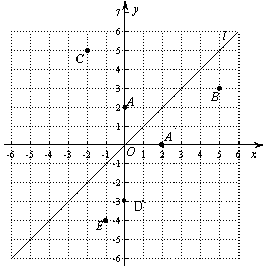

已知y=y₁y₂，y₁与x成正比例，y₂与x+3成反比例，当x="0" 时，y=2；当x=3时，y=2；求y与x的函数关系式。

已知与成反比例，并且当时。
（1）写出与之间的函数解析式；
（2）判断点、、在不在这个函数的图象上？

已知，点P(x，y)在第一象限，且x+y=12，点A(10，0)在x轴上，设△OPA的面积 为S．
求S关于x的关系式，并确定x的取值范围；
当△OPA为直角三角形时，求P点的坐标．
                    

一辆货车在A处加满油后匀速行驶，下表记录的是货车一次加满油后油箱内余油量（升）与行驶时间（时）之间的关系：

行驶时间（时）	0	1	2	2.5
余油量（升）	100	80	60	50

 
求与之间的函数关系式
求货车行驶4.2小时到达B处时油箱内的余油量

已知,与＋1成正比例，与＋1成反比例，当＝0时，＝－5；当＝2时，＝－7。求与的函数关系式

丁丁想在一个矩形材料中剪出

如图阴影所示的梯形，作为要制作的风筝的一个翅膀．
请你根据图中的数据帮丁丁计算出BE、CD的长度
（结果精确到个位，）．

为了预防流感，某校在休息天用药熏消毒法对教室进行消毒．已知药物释放过程中，室内每立方米空气中的含药量y（毫克）与时间t（小时）成正比，药物释放完毕后，y与t的函数关系式为y＝（a为常数），如图所示，根据图中提供的信息，解答下面的问题：
(1)写出从药物释放开始，y与t之间的两个函数关系式及相应的自变量的取值范围；
(2)据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室?

如图①，李老师设计了一个探究杠杆平衡条件的实验：在一个自制类似天平的仪器的左边固定托盘A中放置一个重物，在右边的活动托盘B（可左右移动）中放置一定质量的砝码，使得仪器左右平衡，改变活动托盘B与点O的距离x(cm)，观察活动托盘B中砝码的质量y(g)的变化情况，实验数据记录如下表：

(1)把上表中(x，y)的各组对应值作为点的坐标，在图②中描出相应的点，用平滑曲线连接这些点；
(2)观察所画的图象，猜测y与x之间的函数关系，求出函数关系式并加以验证；
(3)当砝码的质量为24 g时，活动托盘B与点O的距离是多少？
(4)将活动托盘B往左移动时，应往活动托盘B中添加还是减少砝码？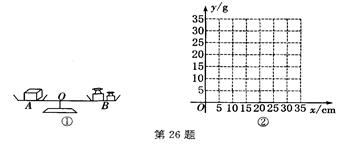

A、B两城间的公路长为450千米，甲、乙两车同时从A城出发沿这一公路驶向B城，甲车到达B城1小时后沿原路返回．如图是它们离A城的路程y（千米）与行驶时间 x（小时）之间的函数图像．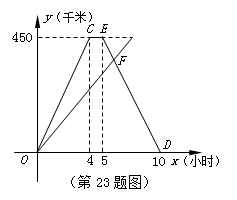

（1）求甲车返回过程中y与x之间的函数解析式，并写出x的取值范围；
（2）乙车行驶6小时与返回的甲车相遇，求乙车的行驶速度．

如图①所示，在直角梯形ABCD中，∠BAD=90°，E是直线AB上一点，过E作直线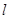//BC，交直线CD于点F．将直线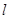向右平移，设平移距离BE为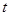(t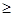0)，直角梯形ABCD被直线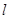扫过的面积（图中阴影部份）为S，S关于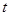的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．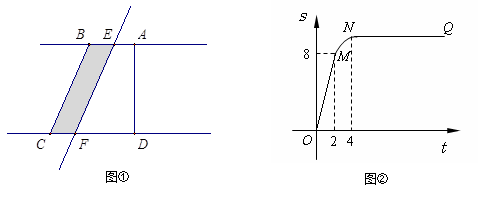

梯形上底的长AB=     
直角梯形ABCD的面积=         
写出图②中射线NQ表示的实际意义；
当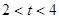时，求S关于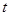的函数关系式；
当t为何值时，直线l将直角梯形ABCD分成的两部分面积之比为1: 3．