如图所示,在平面直角坐标系中,已知A(0,1)B(2,0)C(4,3),
(1)在平面直角坐标系中画出△ABC,并求△ABC的面积
(2)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标。
在平面直角坐标系中,已知P(a,-2)Q(3,b) 且PQ∥x轴,则( )
| A.a=3,b=2 | B.a≠3,b=-2 |
| C.a=-3,b≠-2 | D.a=3,b=-2 |
如图,Rt△ 中,
中, ,
, ,
,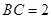 ,
,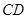 是斜边
是斜边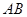 上的高,点
上的高,点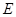 为边
为边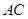 上一点(点
上一点(点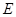 不与点
不与点 、
、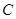 重合),连接
重合),连接 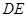 ,作
,作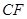 ⊥
⊥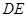 ,
,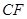 与边
与边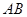 、线段
、线段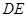 分别交于点
分别交于点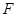 ,
, ;
;
(1)求线段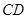 、
、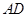 的长;
的长;
(2)设 ,
,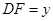 ,求
,求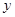 关于
关于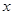 的函数解析式,并写出x的取值范围.
的函数解析式,并写出x的取值范围.
如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.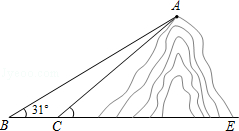
(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31°≈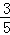 ,sin31°≈
,sin31°≈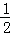 ,tan39°≈
,tan39°≈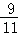 ,sin39°≈
,sin39°≈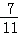 )
)
如图,△ABC中,∠C = 90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ .在整个运动过程中,△MPQ的面积大小变化情况是( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减小
某班数学兴趣小组为了测量建筑物AB与CD的高度,他们选取了地面上点E和建筑物CD的顶端点C为观测点,已知在点C处测得点A的仰角为45°;在点E处测得点C的仰角为30°,测得点A的仰角为37°.又测得DE的长度为9米.
(1)求建筑物CD的高度;
(2)求建筑物AB的高度.(参考数据: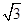 ≈1.73,sin37°≈
≈1.73,sin37°≈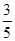 ,cos37°≈
,cos37°≈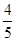 ,tan37°≈
,tan37°≈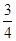 )
)
试题篮
()