用边长为12cm的正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)A方法:剪6个侧面;B方法:剪4侧面5个底面.
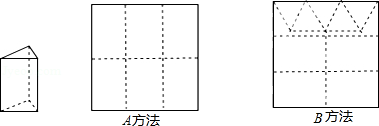
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
①用x的代数式分别表示裁剪出的侧面和底面的个数;
②若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
某市出租车收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米1.3元;超过5千米,每千米2.4元。
(1)若某人乘坐了 (
(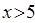 )千米的路程,则他应支付的费用是多少?
)千米的路程,则他应支付的费用是多少?
(2)若某人乘坐的路程为6千米,那么他应支付的费用是多少?
“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向 , 两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥; , 两个果园分别需用110吨和70吨有机化肥.两个仓库到 , 两个果园的路程如表所示:
路程(千米) |
||
甲仓库 |
乙仓库 |
|
果园 |
15 |
25 |
果园 |
20 |
20 |
设甲仓库运往 果园 吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.
运量(吨 |
运费(元 |
|||
甲仓库 |
乙仓库 |
甲仓库 |
乙仓库 |
|
果园 |
|
|
|
|
果园 |
|
|
|
|
(2)设总运费为 元,求 关于 的函数表达式,并求当甲仓库运往 果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
规律探究.下面有8个算式,排成4行2列
2+2, 2×2
3+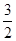 , 3×
, 3×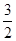
4+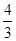 , 4×
, 4×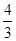
5+ , 5×
, 5× ……, ……
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+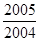 和2005×
和2005×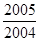 的结果相等吗?
的结果相等吗?
(3)请你试写出算式,试一试,再探索其规律,并用含自然数n的代数式表示这一规律.
将大小不同的两个正方形按如图所示那样拼接起来,连结BD、BF、DF,已知正方形ABCD的边长为 ,正方形CEFG的边长为
,正方形CEFG的边长为 ,且
,且 <
< .
.

(1)填空:BE×DG = (用含 、
、 的代数式表示);
的代数式表示);
(2)当正方形ABCD的边长 保持不变,而正方形CEFG的边长
保持不变,而正方形CEFG的边长 不断增大时,△BDF的面积会发生改变吗?请说明理由.
不断增大时,△BDF的面积会发生改变吗?请说明理由.
某自行车厂计划每天平均生产n辆自行车,而实际产量与计划产量相比有出入.下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
| 星期 |
一 |
二 |
三 |
四] |
五 |
| 实际生产量 |
+5 |
﹣2 |
﹣4 |
+13 |
﹣3 |
(1)用含n的代数式表示本周前三天生产自行车的总数;
(2)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,当n=100时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,当n=100时,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
对任意一个四位数,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
为“极数”.
(1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;
(2)如果一个正整数是另一个正整数
的平方,则称正整数
是完全平方数.若四位数
为“极数”,记
,求满足
是完全平方数的所有
.
某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:①西装和领带都按定价的90%付款;②买一套西装送一条领带.现某客户要到该服装厂购买x套西装(x≥1),领带条数是西装套数的4倍多5.
(1)若该客户按方案①购买,需付款________________元;(用含x的代数式表示)
若该客户按方案②购买,需付款______________ 元。(用含x的代数式表示)
(2)若x=10,通过计算说明此时按哪种方案购买较为合算?
如图所示,已知长方形的长为 米,宽为
米,宽为 米,半圆半径为
米,半圆半径为 米.
米.
(1)这个长方形的面积等于__________平方米;
(2)用代数式表示阴影部分的面积.
对于任意一个四位数 ,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数 为"共生数".例如: ,因为 ,所以3507是"共生数"; ,因为 ,所以4135不是"共生数".
(1)判断5313,6437是否为"共生数"?并说明理由;
(2)对于"共生数" ,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记 .求满足 各数位上的数字之和是偶数的所有 .
对任意一个四位数,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
为“极数”.
(1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;
(2)如果一个正整数是另一个正整数
的平方,则称正整数
是完全平方数.若四位数
为“极数”,记
,求满足
是完全平方数的所有
.
如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为6个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)图中如果点A、B表示的数是互为相反数,那么点A表示的数是 ;
(2)当t=2秒时,点A与点P之间的距离是 个长度单位;
(3)当点A为原点时,点P表示的数是 ;(用含t的代数式表示)
(4)当t= 秒时,点P到点A的距离是点P到点B的距离的2倍.
试题篮
()