礼堂第一排有m个座位,后面每排比前一排多一个座位,则第n排的座位个数有( )
| A.m+n |
| B.mn+1 |
| C.m+(n-1) |
| D.n+(n+1) |
为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度0.45元收费,如果超过140度,超过部分按每度0.60元收费.
(1)若该住户五月份的用电量是100度,则他五月份应交多少电费?
(2)若该住户六月份的用电量是200度,则他六月份应交多少电费?
(3)若某住户七月份的用电量是 度(
度( >140),求这个用户七月份应交多少电费?(结果用含
>140),求这个用户七月份应交多少电费?(结果用含 的式子表示)
的式子表示)
小亮家购买了一套保障房,准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位: ),解答下列问题:
),解答下列问题:
(1)写出用含x、y的代数式表示地面的总面积(结果要化简);
(2)若卫生间和厨房的面积之和是卧室面积的 ,且地面总面积是卫生间面积的15倍,铺1
,且地面总面积是卫生间面积的15倍,铺1 2地砖的平均费用为80元,求铺地砖的总费用为多少元?
2地砖的平均费用为80元,求铺地砖的总费用为多少元?
观察下列等式:
1、42-12=3×5;
2、52-22=3×7;
3、62-32=3×9;
4、72-42=3×11;
…
则第n(n是正整数)个等式为 .
甲、乙两家文具商店出售同样的钢笔和本子.钢笔每支18元,本子每本2元.甲商店推出的优惠方法为买一支钢笔送两本本子;乙商店的优惠方法为按总价的九折优惠.小丽想购买5支钢笔,本子 本(
本( ≥10)
≥10)
(1)若到甲商店购买,应付 元(用代数式表示).
(2)若到乙商店购买,应付 元(用代数式表示).
(3)若小丽要买本子10本,应选择那家商店?若买100本呢?
规律探究.下面有8个算式,排成4行2列
2+2, 2×2
3+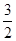 , 3×
, 3×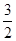
4+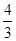 , 4×
, 4×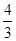
5+ , 5×
, 5× ……, ……
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+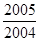 和2005×
和2005×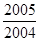 的结果相等吗?
的结果相等吗?
(3)请你试写出算式,试一试,再探索其规律,并用含自然数n的代数式表示这一规律.
某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米 元;超过部分每立方米 元.该地区某用户上月用水量为20立方米,则应缴水费为
| A. |
元 |
B. |
元 |
C. |
元 |
D. |
元 |
“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向 , 两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥; , 两个果园分别需用110吨和70吨有机化肥.两个仓库到 , 两个果园的路程如表所示:
路程(千米) |
||
甲仓库 |
乙仓库 |
|
果园 |
15 |
25 |
果园 |
20 |
20 |
设甲仓库运往 果园 吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.
运量(吨 |
运费(元 |
|||
甲仓库 |
乙仓库 |
甲仓库 |
乙仓库 |
|
果园 |
|
|
|
|
果园 |
|
|
|
|
(2)设总运费为 元,求 关于 的函数表达式,并求当甲仓库运往 果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
某企业今年3月份产值为 a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
| A. |
(a﹣10%)(a+15%)万元 |
B. |
a(1﹣90%)(1+85%)万元 |
| C. |
a(1﹣10%)(1+15%)万元 |
D. |
a(1﹣10%+15%)万元 |
如图,将边长为 的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长 的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为

| A. |
|
B. |
|
C. |
|
D. |
|
观察下列顺序排列的等式:9 0+1=1,9
0+1=1,9 1+2=11,9
1+2=11,9 2+3=21,9
2+3=21,9 3+4=31,9
3+4=31,9 +5=41,……
+5=41,……
根据以上所反映的规律,猜想,第n个等式(n为正整数)应为( )
| A.9(n-1)+n=10(n-1)+1 |
| B.9n+n=(n-1)+n |
| C.9n+(n-1)=n2 -1 |
| D.9n+n=10n+1 |
试题篮
()