如图,正方形 的边长为2,其面积标记为 ,以 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为 , ,按照此规律继续下去,则 的值为

A. B. C. D.
把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形, ,按此规律排列下去,则第⑤个图案中黑色三角形的个数为

A.10B.15C.18D.21
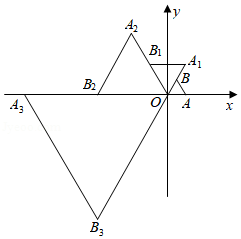
在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到△ ,第二次旋转后得到△ , ,依次类推,则点 的坐标为
| A. |
, |
B. |
, |
| C. |
, |
D. |
, |
观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图 ;对剩下的三个小三角形再分别重复以上做法, 将这种做法继续下去(如图2,图 ,则图6中挖去三角形的个数为

A.121B.362C.364D.729
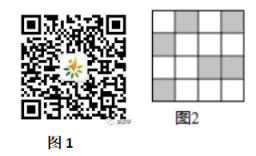
利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 ,如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是
A. B.
B.
C. D.
D.
如图所示,一动点从半径为2的 上的 点出发,沿着射线 方向运动到 上的点 处,再向左沿着与射线 夹角为 的方向运动到 上的点 处;接着又从 点出发,沿着射线 方向运动到 上的点 处,再向左沿着与射线 夹角为 的方向运动到 上的点 处; 按此规律运动到点 处,则点 与点 间的距离是

A.4B. C.2D.0
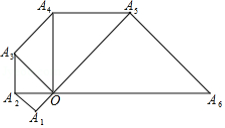
如图,△ 为等腰直角三角形, ,以斜边 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 , ,按此规律作下去,则 的长度为
A. B. C. D.
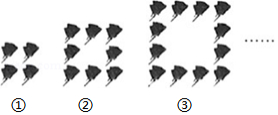
如图所示,下列图形都是由相同的玫瑰花按照一定的规律摆成的,按此规律摆下去,第 个图形中有120朵玫瑰花,则 的值为
A.28B.29C.30D.31
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作; 根据以上操作,若要得到100个小三角形,则需要操作的次数是

A.25B.33C.34D.50
人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成,如图中的每一个小正方形表示一块地砖.如果按图①②③ 的次序铺设地砖,把第 个图形用图 表示,那么第50个图形中的白色小正方形地砖的块数是

A.150B.200C.355D.505
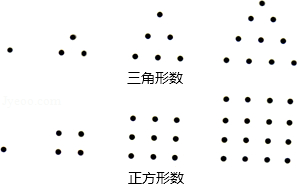
我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为 ,最大的“正方形数”为 ,则 的值为
A.33B.301C.386D.571
试题篮
()