将黑色圆点按如图所示的规律进行排列:

图中黑色圆点的个数依次为:1,3,6,10, ,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为 .
某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
观察思考
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图 ;当正方形地砖有2块时,等腰直角三角形地砖有8块(如图 ;以此类推.

规律总结
(1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加 块;
(2)若一条这样的人行道一共有 为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 (用含 的代数式表示).
问题解决
(3)现有2021块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖多少块?
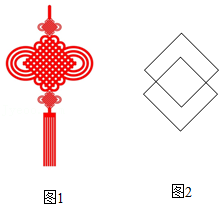
数学兴趣小组同学从"中国结"的图案(图 中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是
| A. |
用3个相同的菱形放置,最多能得到6个菱形 |
| B. |
用4个相同的菱形放置,最多能得到16个菱形 |
| C. |
用5个相同的菱形放置,最多能得到27个菱形 |
| D. |
用6个相同的菱形放置,最多能得到41个菱形 |
如图,正方形 中, , 与直线 所夹锐角为 ,延长 交直线 于点 ,作正方形 ,延长 交直线 于点 ,作正方形 ,延长 交直线 于点 ,作正方形 ,依此规律,则线段 .

如图,菱形 中, , ,延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ;再延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到△ 按此规律,得到△ ,记 的面积为 ,△ 的面积为 ,△ 的面积为 ,则 .

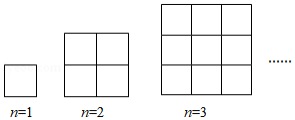
如图中的三个图形都是边长为1的小正方形组成的网格,其中第一个图形有 个小正方形,所有线段的和为4,第二个图形有 个小正方形,所有线段的和为12,第三个图形有 个小正方形,所有线段的和为24,按此规律,则第 个网格中所有线段的和为 (用含 的代数式表示)
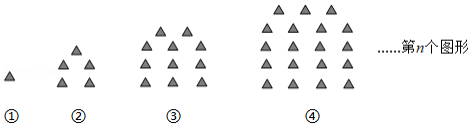
下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形 依此规律,则第 个图形中三角形个数是 .
如图,第(1)个多边形由正三角形“扩展”而来,边数记为 ,第(2)个多边形由正方形 “扩展”而来,边数记为
,第(2)个多边形由正方形 “扩展”而来,边数记为 ,…,依此类推,由正
,…,依此类推,由正 边形“扩展”而来的多边形的边数记为
边形“扩展”而来的多边形的边数记为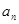 (n≥3).则
(n≥3).则 的值是 ,当
的值是 ,当 的结果是
的结果是 时,n的值 .
时,n的值 .
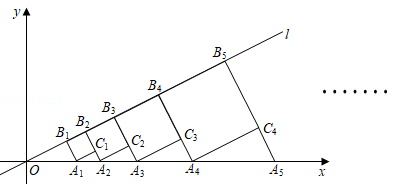
如图,点 在直线 上,点 的横坐标为2,过点 作 ,交 轴于点 ,以 为边,向右作正方形 ,延长 交 轴于点 ;以 为边,向右作正方形 ,延长 交 轴于点 ;以 为边,向右作正方形 ,延长 交 轴于点 ; ;照这个规律进行下去,则第 个正方形 的边长为
(结果用含正整数 的代数式表示).
如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍;拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍; 照这样拼图,则第 个图形需要 根火柴棍.

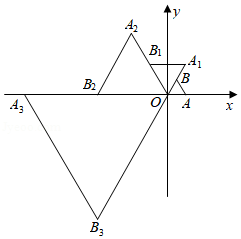
在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到△ ,第二次旋转后得到△ , ,依次类推,则点 的坐标为
| A. |
, |
B. |
, |
| C. |
, |
D. |
, |
在2020年新冠肺炎疫情期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全班同学共通过多少次电话呢?我们可以用下面的方式来解决问题.
用点A1、A2、A3…A48分表示第1名同学、第2名同学、第3名同学…第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:

(1)填写上图中第四个图中y的值为 ,第五个图中y的值为 .
(2)通过探索发现,通电话次数y与该班级人数x之间的关系式为 ,当 时,对应的y= .
(3)若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?
试题篮
()