初中数学规律型：图形的变化类试题

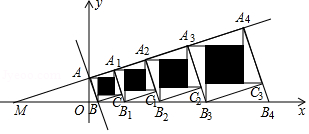
如图，直线 $y=\frac{1}{3}x+1$与 $x$轴交于点 $M$，与 $y$轴交于点 $A$，过点 $A$作 $\mathit{AB}\perp \mathit{AM}$，交 $x$轴于点 $B$，以 $\mathit{AB}$为边在 $\mathit{AB}$的右侧作正方形 $\mathit{ABC}{A}_1$，延长 $A_{1}C$交 $x$轴于点 $B_1$，以 $A_1{B}_1$为边在 $A_1{B}_1$的右侧作正方形 $A_1{B}_1{C}_1{A}_2\dots$按照此规律继续作下去，再将每个正方形分割成四个全等的直角三角形和一个小正方形，每个小正方形的每条边都与其中的一条坐标轴平行，正方形 $\mathit{ABC}{A}_1$， $A_1{B}_1{C}_1{A}_2$， $\dots$， $A_{n-1}{B}_{n-1}{C}_{n-1}{A}_n$中的阴影部分的面积分别为 $S_1$， $S_2$， $\dots$， $S_n$，则 $S_n$可表示为　　．

小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案（如图所示），每个图案中他只在最下面的正方体上写“心”字，寓意“不忘初心”．其中第（1）个图案中有1个正方体，第（2）个图案中有3个正方体，第（3）个图案中有6个正方体， $\dots$按照此规律，从第 $\left(100\right)$个图案所需正方体中随机抽取一个正方体，抽到带“心”字正方体的概率是 $($　　 $)$

A． $\frac{1}{100}$B． $\frac{1}{20}$C． $\frac{1}{101}$D． $\frac{2}{101}$

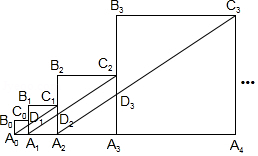
如图，正方形 $A_0{B}_0{C}_0{A}_1$的边长为1，正方形 $A_1{B}_1{C}_1{A}_2$的边长为2，正方形 $A_2{B}_2{C}_2{A}_3$的边长为4，正方形 $A_3{B}_3{C}_3{A}_4$的边长为 $8\dots \dots$依此规律继续作正方形 $A_n{B}_n{C}_n{A}_{n+1}$，且点 $A_0$， $A_1$， $A_2$， $A_3$， $\dots$， $A_{n+1}$在同一条直线上，连接 $A_0{C}_1$交 $A_1{B}_1$于点 $D_1$，连接 $A_1{C}_2$交 $A_2{B}_2$于点 $D_2$，连接 $A_2{C}_3$交 $A_3{B}_3$于点 $D_3\dots \dots$记四边形 $A_0{B}_0{C}_0{D}_1$的面积为 $S_1$，四边形 $A_1{B}_1{C}_1{D}_2$的面积为 $S_2$，四边形 $A_2{B}_2{C}_2{D}_3$的面积为 $S_3\dots \dots$四边形 $A_{n-1}{B}_{n-1}{C}_{n-1}{D}_n$的面积为 $S_n$，则 $S_{2019}=$　　．

如图所示，将形状大小完全相同的“ $▱$”按照一定规律摆成下列图形，第1幅图中“ $▱$”的个数为 $a_1$，第2幅图中“ $▱$”的个数为 $a_2$，第3幅图中“ $▱$”的个数为 $a_3$， $\dots$，以此类推，若 $\frac{2}{a_1}+\frac{2}{a_2}+\frac{2}{a_3}+\dots +\frac{2}{a_n}=\frac{n}{2020}$． $(n$为正整数），则 $n$的值为　　．

刘莎同学用火柴棒依图的规律摆六边形图案，用10086根火柴棒摆出的图案应该是第　　个．

如图，已知 $\angle \mathit{AOB}=30°$，在射线 $\mathit{OA}$上取点 $O_1$，以 $O_1$为圆心的圆与 $\mathit{OB}$相切；在射线 $O_{1}A$上取点 $O_2$，以 $O_2$为圆心， $O_2{O}_1$为半径的圆与 $\mathit{OB}$相切；在射线 $O_{2}A$上取点 $O_3$，以 $O_3$为圆心， $O_3{O}_2$为半径的圆与 $\mathit{OB}$相切； $\dots$；在射线 $O_{9}A$上取点 $O_{10}$，以 $O_{10}$为圆心， $O_{10}{O}_9$为半径的圆与 $\mathit{OB}$相切．若 $\odot O_1$的半径为1，则 $\odot O_{10}$的半径长是　　．

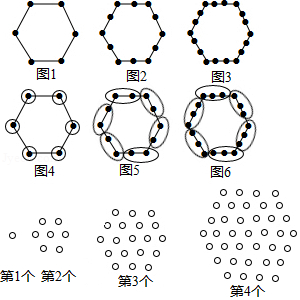
如图，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成； $\dots$按照此规律，第 $n$个图中正方形和等边三角形的个数之和为　　个．

“分块计数法”：对有规律的图形进行计数时，有些题可以采用“分块计数”的方法．

例如：图1有6个点，图2有12个点，图3有18个点， $\dots \dots$，按此规律，求图10、图 $n$有多少个点？

我们将每个图形分成完全相同的6块，每块黑点的个数相同（如图），这样图1中黑点个数是 $6\times 1=6$个；图2中黑点个数是 $6\times 2=12$个：图3中黑点个数是 $6\times 3=18$个； $\dots \dots$；所以容易求出图10、图 $n$中黑点的个数分别是　　、　　．

请你参考以上“分块计数法”，先将下面的点阵进行分块，再完成以下问题：

（1）第5个点阵中有　　个圆圈；第 $n$个点阵中有　　个圆圈．

（2）小圆圈的个数会等于271吗？如果会，请求出是第几个点阵．

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=5$， $\mathit{AC}=4$，若进行以下操作，在边 $\mathit{BC}$上从左到右依次取点 $D_1$、 $D_2$、 $D_3$、 $D_4$、 $\dots$；过点 $D_1$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_1$、 $F_1$；过点 $D_2$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_2$、 $F_2$；过点 $D_3$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_3$、 $F_3\dots$，则 $4(D_1{E}_1+D_2{E}_2+\dots +D_{2019}{E}_{2019})+5(D_1{F}_1+D_2{F}_2+\dots +D_{2019}{F}_{2019})=$　        　．

如图，已知 $\mathit{AB}=A_{1}B$， $A_1{B}_1=A_1{A}_2$， $A_2{B}_2=A_2{A}_3$， $A_3{B}_3=A_3{A}_4\dots$，若 $\angle A=70°$，则 $\angle A_{n-1}{A}_n{B}_{n-1}$的度数为 $($　　 $)$

A． $\frac{70}{2^n}$B． $\frac{70}{2^{n+1}}$C． $\frac{70}{2^{n-1}}$D． $\frac{70}{2^{n+2}}$

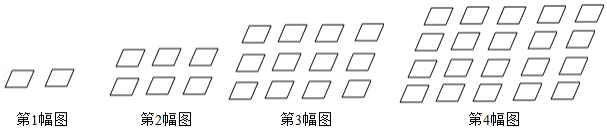
海南黎锦有着悠久的历史，已被列入世界非物质文化遗产名录．如图是黎锦上的图案，每个图案都是由相同菱形构成的，若按照第1个图至第4个图中的规律编织图案，则第5个图中有　　个菱形，第 $n$个图中有　　个菱形（用含 $n$的代数式表示）．

下面图形都是由同样大小的小球按一定规律排列的，依照此规律排列下去，第   

　　个图形共有210个小球．

某广场用同一种如图所示的地砖拼图案，第一次拼成形如图1所示的图案，第二次拼成形如图2所示的图案，第三次拼成形如图3所示的图案，第四次拼成形如图4所示的图案 $\dots$按照这样的规律进行下去，第 $n$次拼成的图案共用地砖　　块．

下列图形都是由同样大小的实心圆点按一定规律组成的，其中第①个图形一共有5个实心圆点，第②个图形一共有8个实心圆点，第③个图形一共有11个实心圆点，…，按此规律排列下去，第⑥个图形中实心圆点的个数为（　　）

A．

$18$

B．

$19$

C．

$20$

D．

$21$

下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案①需8根火柴棒，图案②需15根火柴棒， $\dots$，按此规律，图案⑦需　　根火柴棒．