初中数学幂的乘方与积的乘方试题

一辆货车从超市出发，向东走了2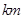到达小刚家，继续向东走了3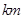到达小红家，又向西走了9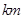到达小英家，最后回到超市．
（1）请以超市为原点，以向东方向为正方向，用1个单位长度表示1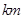，画出数轴，在数轴上表示出小刚家、小红家、小英家的位置；
（2）小英家距小刚家有多远？
（3）货车一共行驶了多少千米？

如图，数轴的单位长度为1．

（1）如果点B，D表示的数互为相反数，那么图中点A、点D表示的数分别是    、      ；
（2）当点B为原点时，在数轴上是否存在点M，使得点M到点A的距离是点M到点D的距离的2倍，若存在，请求出此时点M所表示的数；若不存在，说明理由；
（3） 在（2）的条件下，点A、点C分别以2个单位长度/秒和0.5个单位长度同时向右运动，同时点P从原点出发以3个单位长度/秒的速度向左运动，当点A与点C之间的距离为3个单位长度时，求点P所对应的数是多少？

探索规律观察下面由※组成的图案和算式，解答问题

（1）请计算1+3+5+7+9+11=__________；
（2）请猜想1+3+5+7+9+…+19=__________；
（3）请猜想1+3+5+7+9+…+（2n﹣1）=__________；
（4）请用上述规律计算：21+23+25+…+99．

如图，按此规律，第      行最后一个数是2017．

观察下图的变化规律，在第n个图中，三角形的个数为_______

从2开始，连续的偶数相加，它们和的情况如下表：

加数的个数n	S
1	2=1×2
2	2＋4=6=2×3
3	2＋4＋6=12=3×4
4	2＋4＋6＋8=20=4×5
5	2＋4＋6＋8＋10=30=5×6

 
（1）若n=8时，则S的值为_____________．
（2）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=__________________．
（3）根据上题的规律计算2+4+6+8+10+…+98+100的值．

观察下面的一列数，按某种规律在横线上填上适当的数：
______…，第100个数是_________，这100个数的和为________．

如图，数轴上的A、B、C、D四点所表示的数分别为a、b、c、d，且O为原点．根据图中各点位置，判断|a－c|之值与下列选项中哪个不同（ ）

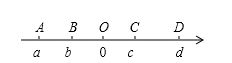
A．|a－b|+|c－b|            B．|a|+|d|-|c+d|
C．|a－d|－|d－c|           D．|a|+|d|－|c－d|

如图，正方形ABCD的边长为12，划分成12×12个小正方形格．将边长为n（n为整数，且2≤n≤11）的黑白两色正方形纸片按图中的方式黑白相间地摆放，第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格，第二张纸片盖住第一张纸片的部分恰好为（n﹣1）×（n﹣1）的正方形．如此摆放下去，最后直到纸片盖住正方形ABCD的右下角为止．

请你认真观察思考后回答下列问题：
（1）由于正方形纸片边长n的取值不同，完成摆放时所使用正方形纸片的张数也不同，请填写下表：

纸片的边长n	2	3	4	5	6
使用的纸片张数

（2）设正方形ABCD被纸片盖住的面积（重合部分只计一次）为S₁，未被盖住的面积为S₂．
①当n=2时，求S₁：S₂的值；
②用含n的代数式表示S₂．

设a，b，c是从1到9的互不相同的整数，则的最大值为      ．

假设一家旅馆一共有30个房间，分别编以1-30号三十个号码，现在要在每个房间的钥匙上刻上数字，要求所刻数字必须使服务员很容易辨认是哪一个房间的钥匙，而使外人不容易猜到，现在有一种编码方法是：在每把钥匙上刻上两个数字，左边的一个数字是这把钥匙原来的房间号除以5所得的余数，而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数，那么刻的数是36的钥匙所对应的原来房间应该是___________号．

2015年9月30日杭州西湖景区某公园人流量为7万，每张门票80元，“十一黄金周”景区迎来了旅游高峰期，游客从各个省市来到杭州，该公园统计：十一黄金周期间，游客人数与前一天相比，增加和减少的情况如下表：（记增加为正）．

日期	1号	2号	3号	4号	5号	6号	7号
人数（万人）	+5	-1．2	+5．7	-0．6	+1．8	-2．9	-2．5

 
（1）10月2号该公园的人流量是多少万人？
（2）“十一黄金周”期间，人流量最多和最少分别出现在哪一天？
（3）该公园的所有门票收入均要缴纳百分之五的税，求“十一黄金周”期间，该公园的实际收入．

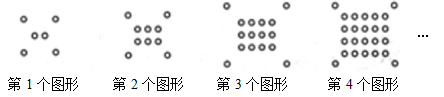
将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，……依次规律，第6个图形有       个小圆。

平移小菱形◇可以得到美丽的“中国结”图案，下面四个图案是由◇平移后得到的类似“中国结”的图案，按图中规律，第20个图案中，小菱形的个数是          个．

数学家发明了一个魔术盒，当任意数对（a，b）放入其中时，会得到一个新的数：a²+b+1．例如把（3，﹣2）放入其中，就会得到3²+（﹣2）+1=8．现将数对（﹣2，3）放入其中得到数m=      ，再将数对（m，1）放入其中后，得到的数是      ．