初中数学幂的乘方与积的乘方试题

（本题6分）阅读理解：
图1中的每相邻两条竖线之间，从上至下有若干条横线（即“桥”），这样就构成了“天梯”。现在规定，运算符号“×、÷、+、－”分别从它们下方的竖线上端出发，在“天梯”的竖线与横线上运动，它们在运动过程中按自上而下，且逢“桥”必过的规则进行，最后运动到竖线下方字母之间的“○”中，将a、b、c、d、e连接起来，构成一个算式．例如图1中，“×”号根据规则就应该沿箭头方向运动，最后向下进入d、e之间的“○”中，其余3个运算符号分别按规则运动到“○”中后，就得到算式：a－b+c÷d×e．
解决问题：
（1）根据图2所示的“天梯”写出算式，并计算当a=6，b=﹣3²，c=﹣8，d=，e=﹣时所写算式的值；
（2）在图3添加横线（不超过4条），中设计出一种“天梯”，使列出的算式为a－b÷c×d+e．

（本小题10分）（1）观察一列数a₁＝3，a₂＝3²，a₃＝3³，a₄＝3⁴，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是_______；根据此规律，如果a_n（n为正整数）表示这个数列的第n项，那么a₆＝_______，a_n＝_______；（可用幂的形式表示）
（2）如果想要求l＋2＋2²＋2³＋．．．＋2¹⁰的值，可令S₁₀＝l＋2＋2²＋2³＋．．．＋2¹⁰，①将①式两边同乘以2，得_______②，由②减去①式，得S₁₀＝_______．
（3）若（1）中数列共有20项，设S₂₀＝3＋3²＋3³＋3⁴＋…＋a₂₀，请利用上述规律和方法计算S₂₀的值．

假设一家旅馆一共有30个房间，分别编以1-30号三十个号码，现在要在每个房间的钥匙上刻上数字，要求所刻数字必须使服务员很容易辨认是哪一个房间的钥匙，而使外人不容易猜到，现在有一种编码方法是：在每把钥匙上刻上两个数字，左边的一个数字是这把钥匙原来的房间号除以5所得的余数，而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数，那么刻的数是36的钥匙所对应的原来房间应该是___________号．

亚奥理事会于2015年9月16日在土库曼斯坦阿什哈巴德举行第34届代表大会，并在会上投票选出2022年第19届亚运会举办城市为杭州．5个城市的国际标准时间（单位：时）在数轴上表示如图所示，那么北京时间2015年9月16日20时应是（   ）

A．伦敦时间2015年9月16日11时

B．巴黎时间2015年9月16日13时

C．智利时间2015年9月16日5时

D．曼谷时间2015年9月16日18时

如图，按此规律，第      行最后一个数是2017．

如图，图1中共有5个三角形，在图2中共有         个三角形，在图3中共有    个三角形 ……在第8个图形中共有           个三角形．

在某次抗险救灾中，消防官兵的冲锋舟沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B 地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：
+12，﹣9，+8，﹣7，+11，﹣6，+10，﹣5．
（1）B地在A地什么方向，距离A地多少千米？
（2）若冲锋舟每千米耗油0．5升，油箱容量为30升，求途中还需补充多少升油．

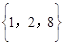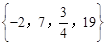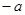把几个数用大括号括起来，中间用逗号断开，如：、，我们称之为集合，其中的数称其为集合的元素．如果一个集合满足：当有理数是集合的元素时，有理数10也必是这个集合的元素，这样的集合我们称为“好的集合”．例如集合｛10，0｝就是一个“好的集合”．
（1）集合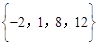        （填“是”或“不是”）“好的集合”．
（2）请你再写出两个好的集合（不得与上面出现过的集合重复）．
（3）在所有“好的集合”中，元素个数最少的集合是        ．

设a，b，c是从1到9的互不相同的整数，则的最大值为      ．

阅读下列材料，并解决相关的问题．
按照一定顺序排列着的一列数称为数列，排在第一位的数称为第1项，记为，依次类推，排在第位的数称为第项，记为．
一般地，如果一个数列从第二项起，每一项与它前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母表示（）．如：数列1，3，9，27，…为等比数列，其中，公比为．
则：（1）等比数列3，6，12，…的公比为            ，第4项是               ．
（2）如果一个数列，，，，…是等比数列，且公比为，那么根据定义可得到：
，，，…… ．
所以：，，，
由此可得：                   （用和的代数式表示）
（3）若一等比数列的公比q=2，第2项是10，请求它的第1项与第4项．

我们把所有正奇数按照从小到大的顺序排列，并按如下规律分组：（1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…现用等式An=（a，b）表示奇数x是第a组第b个数（从左往右数），如A₇=（2，3），A₂₃=（4，4），则A₂₀₁₅=          ．

读一读：
式子“1+2+3+4+5+…+100”表示从1开始的100个连续自然数的和．
由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“1+2+3+4+5+…+100”表示为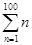，这里“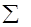”是求和符号．例如：“1+3+5+7+9+…+99”（即从1开始的100以内连续奇数的和）可表示为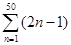；又如“1³+2³+3³+4³+5³+6³+7³+8³+9³+10³”可表示为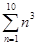． 同学们，通过对以上材料的阅读，请解答下列问题：
（1）“2+4+6+8+10+…+100”（即从2开始的100以内的连续偶数的和）用求和符号可表示为              ．
（2）计算: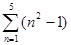的值

将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，……依次规律，第6个图形有       个小圆。

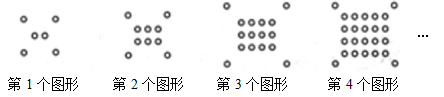
观察图，解答下列问题．

（1）图中的小圆圈被折线隔开分成六层，第一层有1个小圆圈，第二层有3个圆圈，第三层有5个圆圈，……，第六层有11个圆圈．如果要你继续画下去第n层 有          圆圈
（2）某一层上有65个圆圈，这是第          层
（3）数图中的圆圈个数可以有多种不同的方法．
比如：前两层的圆圈个数和为（1+3）或2²，
由此得，1+3 = 2²．
同样，
由前三层的圆圈个数和得：1+3+5 = 3²．
由前四层的圆圈个数和得：1+3+5+7 = 4²．
由前五层的圆圈个数和得：1+3+5+7+9 = 5²．
……
根据上述请你猜测，从1开始的n个连续奇数之和是多少？用公式把它表示出来．
（4）计算：1+3+5+…+299的和；
（5）计算：101+103+105+…+299的和．

数学家发明了一个魔术盒，当任意数对（a，b）放入其中时，会得到一个新的数：a²+b+1．例如把（3，﹣2）放入其中，就会得到3²+（﹣2）+1=8．现将数对（﹣2，3）放入其中得到数m=      ，再将数对（m，1）放入其中后，得到的数是      ．