点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a－b|．
利用数形结合思想回答下列问题：
（1）数轴上表示2和10两点之间的距离是_________，数轴上表示2和－10的两点之间的距离是______．
（2）数轴上表示x和－2的两点之间的距离表示为____________．
（3）若x表示一个有理数， |x－1|+|x+2|有最小值吗？若有，请求出最小值，若没有，写出理由．
（4）若x表示一个有理数，求|x－1|+|x－2|+|x－3|+|x－4|+……+|x－2014|+|x－2015|的最小值．
用黑白两种颜色正方形的纸片按黑色纸片数逐渐加l的规律拼成一列图案：第n个图案中有白色纸片___________张．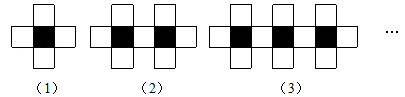
如图，是一组按照某种规律摆放而成的图案，第1个图有1个三角形，第二个图有4个三角形，第三个图有8个三角形，第四个图有12个三角形，则图5中三角形的个数是（ ）
| A．8 | B．12 | C．16 | D．17 |
在求两位数的平方时，可以用“列竖式”的方法进行速算，求解过程如图1所示．
（1）仿照图1，在图2中补全672的“竖式”；
（2）仿照图1，用“列竖式”的方法计算一个两位数的平方，部分过程如图3所示．若这个两位数的个位数字为a，则这个两位数为 （用含a的代数式表示）．
如图，在数轴上A点表示数﹣2，B点表示数6，若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，则经过 秒，甲、乙两小球到原点的距离相等．
设[x）表示大于x的最小整数，如[3）＝4，[－1．2）＝－1，则下列结论中正确的是_______．（填写所有正确结论的序号）①[0）＝0；②[x）－x的最小值是0；③[x）－x的最大值是0；④存在实数x，使[x）－x＝0．5成立。
探索规律：
观察由※组成的图案和算式，解答问题：
1+3=4=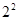
1+3+5=9=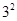
1+3+5+7=16=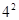
1+3+5+7+9=25=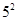
（1）请猜想1+3+5+7+9+ … +29= ；
（2）请猜想1+3+5+7+9+ … +（2n-1）+（2n+1）= ；
（3）请用上述规律计算：41+43+45+ …… +77+79
将自然数按以下规律排列：
第一列 第二列 第三列 第四列 第五列
第一行 1 4 5 16 17
第二行 2 3 6 15 …
第三行 9 8 7 14 …
第四行 10 11 12 13 …
第五行 …
表中数2在第二行，第一列，与有序数对（2,1）对应；数5与（1,3）对应；数14与（3,4）对应，根据这一规律，数2014对应的有序数对为 .
如图，图1中共有5个三角形，在图2中共有 个三角形，在图3中共有 个三角形 ……在第8个图形中共有 个三角形．
股民小万上周五以前以每股13元的价格买进某种股票10000股，该股票这周内与前一天相比的涨跌情况如下表（单位：元）
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
+0．6 |
-0．4 |
-0．2 |
+0．5 |
+0．3 |
（1）本周内哪一天把股票抛出比较合算？为什么？
（2）已知小万买进股票时付了3‰的手续费，卖出时需付成交额3‰的手续费和2‰的交易税，如果小万在星期五收盘前将全部股票卖出，他的收益情况如何？（注：3‰表示千分之三）
观察图，解答下列问题．
（1）图中的小圆圈被折线隔开分成六层，第一层有1个小圆圈，第二层有3个圆圈，第三层有5个圆圈，……，第六层有11个圆圈．如果要你继续画下去第n层 有 圆圈
（2）某一层上有65个圆圈，这是第 层
（3）数图中的圆圈个数可以有多种不同的方法．
比如：前两层的圆圈个数和为（1+3）或22，
由此得，1+3 = 22．
同样，
由前三层的圆圈个数和得：1+3+5 = 32．
由前四层的圆圈个数和得：1+3+5+7 = 42．
由前五层的圆圈个数和得：1+3+5+7+9 = 52．
……
根据上述请你猜测，从1开始的n个连续奇数之和是多少？用公式把它表示出来．
（4）计算：1+3+5+…+299的和；
（5）计算：101+103+105+…+299的和．
数学家发明了一个魔术盒，当任意数对（a，b）放入其中时，会得到一个新的数：a2+b+1．例如把（3，﹣2）放入其中，就会得到32+（﹣2）+1=8．现将数对（﹣2，3）放入其中得到数m= ，再将数对（m，1）放入其中后，得到的数是 ．
试题篮
()
粤公网安备 44130202000953号
______…，第100个数是_________，这100个数的和为________．
的最大值为 ．
，
，
，
，……，第2012个数是_____________；