初中数学多项式乘多项式试题

若，则a、b的值为

A．a=5，b=6

B．a=1，b=−6

C．a=1，b=6

D．a=5，b=−6

如图甲是一个长2m，宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图乙的形状拼成一个正方形．
（1）求图乙中阴影部分的面积．
（2）观察图乙，请你写出三个代数式、、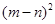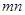之间的等量关系式．
（3）根据（2）中的结论，若，，求的值．
（4）有许多代数恒等式可以用图形的面积来表示．如图丙，它表示了．
试画一个几何图形，使它的面积能表示：．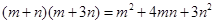

若（x+m）与（x+3）的乘积中不含x的一次项，则m=               ．

阅读下文，寻找规律．计算
,
,
……．
（1）观察上式，并猜想：                 ．
（2）根据你的猜想，计算:                  ．（其中n是正整数）

长方形相邻两边的长分别是与，那么这个长方形的面积是（     ）

A．	B．
C．	D．

两整式相乘的结果为a²－a－12的是（   ）

A．（a－6）（a+2）	B．（a－3）（a+4）
C．（a+6）（a－2）	D．（a+3）（a－4）

若，则的值为         ．

若（x－3）（x+4）=x²+px+q，那么p、q的值是（   ）

A．p=1，q=－12	B．p=－1，q=12
C．p=7，q=12	D．p=7，q=－12

如（x＋m）与（x＋3）的乘积中不含x的一次项，则m的值为（ ）．

A．0

B．3

C．－3

D．1

若（3x+a）（3x+b）的结果中不含有x项，则a、b的关系是（  ）

A．ab=1

B．ab=0

C．a—b=0

D．a+b=0

下列各式
（1）    
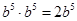
（2）   
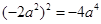
（3）  
（4）
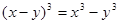
（5）
（6）
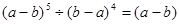
（7）
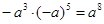
其中计算错误的有 （    ）

A．4个

B．5个

C．6个

D．7个