初中数学一元二次方程的应用试题

2021年是中国共产党建党100周年，全国各地积极开展“弘扬红色文化，重走长征路”主题教育学习活动，我市“红二方面军长征出发地纪念馆”成为重要的活动基地．据了解，今年3月份该基地接待参观人数10万人，5月份接待参观人数增加到12.1万人．

（1）求这两个月参观人数的月平均增长率；

（2）按照这个增长率，预计6月份的参观人数是多少？

据统计，2021年第一季度宜宾市实现地区生产总值约652亿元，若使该市第三季度实现地区生产总值960亿元，设该市第二、三季度地区生产总值平均增长率为 $x$，则可列方程 　　．

有一个人患了流行性感冒，经过两轮传染后共有144人患了流行性感冒，则每轮传染中平均一个人传染的人数是 $($ 　　 $)$

A．

14

B．

11

C．

10

D．

9

“杂交水稻之父” $--$袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标，第三阶段实现水稻亩产量1008公斤的目标．

（1）如果第二阶段、第三阶段亩产量的增长率相同，求亩产量的平均增长率；

（2）按照（1）中亩产量增长率，科研团队期望第四阶段水稻亩产量达到1200公斤，请通过计算说明他们的目标能否实现．

某工厂有甲、乙两个车间，甲车间生产 $A$ 产品，乙车间生产 $B$ 产品，去年两个车间生产产品的数量相同且全部售出．已知 $A$ 产品的销售单价比 $B$ 产品的销售单价高100元，1件 $A$ 产品与1件 $B$ 产品售价和为500元．

（1） $A$ 、 $B$ 两种产品的销售单价分别是多少元？

（2）随着 $5G$ 时代的到来，工业互联网进入了快速发展时期．今年，该工厂计划依托工业互联网将乙车间改造为专供用户定制 $B$ 产品的生产车间．预计 $A$ 产品在售价不变的情况下产量将在去年的基础上增加 $a\%$ ； $B$ 产品产量将在去年的基础上减少 $a\%$ ，但 $B$ 产品的销售单价将提高 $3a\%$ ．则今年 $A$ 、 $B$ 两种产品全部售出后总销售额将在去年的基础上增加 $\frac{29}{25}a\%$ ．求 $a$ 的值．

重庆小面是重庆美食的名片之一，深受外地游客和本地民众欢迎．某面馆向食客推出经典特色重庆小面，顾客可到店食用（简称"堂食"小面），也可购买搭配佐料的袋装生面（简称"生食"小面）．已知3份"堂食"小面和2份"生食"小面的总售价为31元，4份"堂食"小面和1份"生食"小面的总售价为33元．

（1）求每份"堂食"小面和"生食"小面的价格分别是多少元？

（2）该面馆在4月共卖出"堂食"小面4500份，"生食"小面2500份．为回馈广大食客，该面馆从5月1日起每份"堂食"小面的价格保持不变，每份"生食"小面的价格降低 $\frac{3}{4}a\%$ ．统计5月的销量和销售额发现："堂食"小面的销量与4月相同，"生食"小面的销量在4月的基础上增加 $\frac{5}{2}a\%$ ，这两种小面的总销售额在4月的基础上增加 $\frac{5}{11}a\%$ ．求 $a$ 的值．

某服装店以每件30元的价格购进一批 $T$恤，如果以每件40元出售，那么一个月内能售出300件，根据以往销售经验，销售单价每提高1元，销售量就会减少10件，设 $T$恤的销售单价提高 $x$元．

（1）服装店希望一个月内销售该种 $T$恤能获得利润3360元，并且尽可能减少库存，问 $T$恤的销售单价应提高多少元？

（2）当销售单价定为多少元时，该服装店一个月内销售这种 $T$恤获得的利润最大？最大利润是多少元？

在2020年新冠肺炎疫情期间，某中学响应政府有“停课不停学”的号召，充分利用网络资源进行网上学习，九年级1班的全体同学在自主完成学习任务的同时，彼此关怀，全班每两个同学都通过一次电话，互相勉励，共同提高，如果该班共有48名同学，若每两名同学之间仅通过一次电话，那么全班同学共通过多少次电话呢？我们可以用下面的方式来解决问题．

用点A₁、A₂、A₃…A₄₈分表示第1名同学、第2名同学、第3名同学…第48名同学，把该班级人数x与通电话次数y之间的关系用如图模型表示：

（1）填写上图中第四个图中y的值为　　，第五个图中y的值为　　．

（2）通过探索发现，通电话次数y与该班级人数x之间的关系式为　 　，当 $x＝48$时，对应的y＝　   　．

（3）若九年级1班全体女生相互之间共通话190次，问：该班共有多少名女生？

为响应“把中国人的饭碗牢牢端在自己手中”的号召，确保粮食安全，优选品种，提高产量，某农业科技小组对 $A$， $B$两个玉米品种进行实验种植对比研究．去年 $A$、 $B$两个品种各种植了10亩．收获后 $A$、 $B$两个品种的售价均为 $2.4$元/kg，且 $B$品种的平均亩产量比A品种高100千克， $A$、 $B$两个品种全部售出后总收入为 $21600$元．

（1）求 $A$、 $B$两个品种去年平均亩产量分别是多少千克？

（2）今年，科技小组优化了玉米的种植方法，在保持去年种植面积不变的情况下，预计A、B两个品种平均亩产量将在去年的基础上分别增加 $a\%$和 $2a\%$．由于B品种深受市场欢迎，预计每千克售价将在去年的基础上上涨 $a\%$，而A品种的售价保持不变， $A$、 $B$两个品种全部售出后总收入将增加 $\frac{20}{9}a\%$．求a的值．

2021年7月1日是建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数（如图所示），若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数（请用方程知识解答）．

列方程（组 $)$解应用题

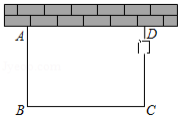
某驻村工作队，为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下，围一块面积为 $600m^2$的矩形试验茶园，便于成功后大面积推广．如图所示，茶园一面靠墙，墙长 $35m$，另外三面用 $69m$长的篱笆围成，其中一边开有一扇 $1m$宽的门（不包括篱笆）．求这个茶园的长和宽．

今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．

（1）求四月和五月这两个月中该景区游客人数平均每月增长百分之几；

（2）若该景区仅有 $A$ ， $B$ 两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	$A$	$B$	$A$ 和     $B$
门票价格	100元     $/$ 人	80元     $/$ 人	160元     $/$ 人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．

①若丙种门票价格下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

某水果商店销售一种进价为40元 $/$千克的优质水果，若售价为50元 $/$千克，则一个月可售出500千克；若售价在50元 $/$千克的基础上每涨价1元，则月销售量就减少10千克．

（1）当售价为55元 $/$千克时，每月销售水果多少千克？

（2）当月利润为8750元时，每千克水果售价为多少元？

（3）当每千克水果售价为多少元时，获得的月利润最大？

列方程（组 $)$解应用题

端午节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：

小王：该水果的进价是每千克22元；

小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低3元，每天的销售量将增加120千克．

根据他们的对话，解决下面所给问题：超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？

“中国人的饭碗必须牢牢掌握在咱们自己手中”．为优选品种，提高产量，某农业科技小组对 $A$， $B$两个小麦品种进行种植对比实验研究．去年 $A$， $B$两个品种各种植了10亩．收获后 $A$， $B$两个品种的售价均为2.4元 $/\mathit{kg}$，且 $B$的平均亩产量比 $A$的平均亩产量高 $100\mathit{kg}$， $A$， $B$两个品种全部售出后总收入为21600元．

（1）请求出 $A$， $B$两个品种去年平均亩产量分别是多少？

（2）今年，科技小组加大了小麦种植的科研力度，在 $A$， $B$种植亩数不变的情况下，预计 $A$， $B$两个品种平均亩产量将在去年的基础上分别增加 $a\%$和 $2a\%$．由于 $B$品种深受市场的欢迎，预计每千克价格将在去年的基础上上涨 $a\%$，而 $A$品种的售价不变． $A$， $B$两个品种全部售出后总收入将在去年的基础上增加 $\frac{20}{9}a\%$．求 $a$的值．