初中数学一元二次方程的应用解答题

一商店销售某种商品，平均每天可售出20件，每件盈利40元．为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．

（1）若降价3元，则平均每天销售数量为　　件；

（2）当每件商品降价多少元时，该商店每天销售利润为1200元？

温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件利润减少2元．设每天安排 $x$人生产乙产品．

（1）根据信息填表：

产品种类	每天工人数（人 $)$	每天产量（件 $)$	每件产品可获利润（元 $)$
甲			15
乙	$x$	$x$

（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．

（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润 $W$（元 $)$的最大值及相应的 $x$值．

根据衢州市统计局发布的统计数据显示，衢州市近5年国民生产总值数据如图1所示，2016年国民生产总值中第一产业，第二产业，第三产业所占比例如图2所示．

请根据图中信息，解答下列问题：

（1）求2016年第一产业生产总值（精确到1亿元）

（2）2016年比2015年的国民生产总值增加了百分之几？（精确到 $1\%)$

（3）若要使2018年的国民生产总值达到1573亿元，求2016年至2018年我市国民生产总值的平均增长率（精确到 $1\%)$

随着某市养老机构（养老机构指社会福利院、养老院、社区养老中心等）建设稳步推进，拥有的养老床位不断增加．

（1）该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个，求该市这两年（从2013年度到2015年底）拥有的养老床位数的平均年增长率；

（2）若该市某社区今年准备新建一养老中心，其中规划建造三类养老专用房间共100间，这三类养老专用房间分别为单人间 $(1$个养老床位），双人间 $(2$个养老床位），三人间 $(3$个养老床位），因实际需要，单人间房间数在10至30之间（包括10和 $30)$，且双人间的房间数是单人间的2倍，设规划建造单人间的房间数为 $t$．

①若该养老中心建成后可提供养老床位200个，求 $t$的值；

②求该养老中心建成后最多提供养老床位多少个？最少提供养老床位多少个？

某烘焙店生产的蛋糕礼盒分为六个档次，第一档次（即最低档次）的产品每天生产76件，每件利润10元．调查表明：生产每提高一个档次的蛋糕产品，该产品每件利润增加2元．

（1）若生产的某批次蛋糕每件利润为14元，此批次蛋糕属第几档次产品；

（2）由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1080元，该烘焙店生产的是第几档次的产品？

某商品的进价为每件40元，售价为每件60元时，每个月可卖出100件；如果每件商品的售价每上涨1元，则每个月少卖2件．设每件商品的售价为 $x$元 $(x$为正整数），每个月的销售利润为 $y$元．

（1）当每件商品的售价是多少元时，每个月的利润刚好是2250元？

（2）当每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

巴中市某楼盘准备以每平方米5000元的均价对外销售，由于有关部门关于房地产的新政策出台后，部分购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4050元的均价开盘销售，若两次下调的百分率相同，求平均每次下调的百分率．

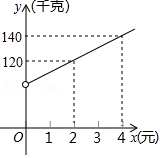
安顺市某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量 $y$（千克）与每千克降价 $x$（元 $\left)\right(0<x<20)$之间满足一次函数关系，其图象如图所示：

（1）求 $y$与 $x$之间的函数关系式；

（2）商贸公司要想获利2090元，则这种干果每千克应降价多少元？

某公司投入研发费用80万元 $(80$万元只计入第一年成本），成功研发出一种产品．公司按订单生产（产量 $=$销售量），第一年该产品正式投产后，生产成本为6元 $/$件．此产品年销售量 $y$（万件）与售价 $x$（元 $/$件）之间满足函数关系式 $y=-x+26$．

（1）求这种产品第一年的利润 $W_1$（万元）与售价 $x$（元 $/$件）满足的函数关系式；

（2）若该产品第一年的利润为20万元，那么该产品第一年的售价是多少？

（3）在（2）的条件下，第二年，该公司将第一年的利润20万元 $(20$万元只计入第二年成本）再次投入研发，使产品的生产成本降为5元 $/$件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过12万件．请计算该公司第二年的利润 $W_2$至少为多少万元．

为积极响应新旧动能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台．假定该设备的年销售量 $y$（单位：台）和销售单价 $x$（单位：万元）成一次函数关系．

（1）求年销售量 $y$与销售单价 $x$的函数关系式；

（2）根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润，则该设备的销售单价应是多少万元？

今年，我市某中学响应习总书记“足球进校园”的号召，开设了“足球大课间”活动，现需要购进100个某品牌的足球供学生使用．经调查，该品牌足球2015年单价为200元，2017年单价为162元．

（1）求2015年到2017年该品牌足球单价平均每年降低的百分率；

（2）选购期间发现该品牌足球在两个文体用品商场有不同的促销方案：

试问去哪个商场购买足球更优惠？

工人师傅用一块长为 $10\mathit{dm}$，宽为 $6\mathit{dm}$的矩形铁皮制作一个无盖的长方体容器，需要将四角各裁掉一个正方形．（厚度不计）

（1）在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；并求长方体底面面积为 $12d{m}^2$时，裁掉的正方形边长多大？

（2）若要求制作的长方体的底面长不大于底面宽的五倍，并在容器外表面进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，裁掉的正方形边长多大时，总费用最低，最低为多少？

列方程解应用题：

某玩具厂生产一种玩具，按照控制固定成本降价促销的原则，使生产的玩具能够及时售出，据市场调查：每个玩具按480元销售时，每天可销售160个；若销售单价每降低1元，每天可多售出2个．已知每个玩具的固定成本为360元，问这种玩具的销售单价为多少元时，厂家每天可获利润20000元？

某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量 $y$（本 $)$与每本纪念册的售价 $x$（元 $)$之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．

（1）请直接写出 $y$与 $x$的函数关系式；

（2）当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？

（3）设该文具店每周销售这种纪念册所获得的利润为 $w$元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？

为满足市场需求，新生活超市在端午节前夕购进价格为3元 $/$个的某品牌粽子，根据市场预测，该品牌粽子每个售价4元时，每天能出售500个，并且售价每上涨0.1元，其销售量将减少10个，为了维护消费者利益，物价部门规定，该品牌粽子售价不能超过进价的 $200\%$，请你利用所学知识帮助超市给该品牌粽子定价，使超市每天的销售利润为800元．