在直角坐标系中,设函数 , 是常数, .
(1)若该函数的图象经过 和 两点,求函数的表达式,并写出函数图象的顶点坐标;
(2)写出一组 , 的值,使函数 的图象与 轴有两个不同的交点,并说明理由.
(3)已知 ,当 , , 是实数, 时,该函数对应的函数值分别为 , .若 ,求证: .
有一电脑程序:每按一次按键,屏幕的 区就会自动加上 ,同时 区就会自动减去 ,且均显示化简后的结果.已知 , 两区初始显示的分别是25和 ,如图.
如,第一次按键后, , 两区分别显示:
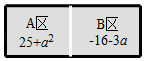
(1)从初始状态按2次后,分别求 , 两区显示的结果;
(2)从初始状态按4次后,计算 , 两区代数式的和,请判断这个和能为负数吗?说明理由.

阅读材料:用配方法求最值.已知x,y为非负实数,
∵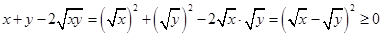
∴ ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求 的最小值.
的最小值.
解: ,当
,当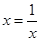 ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求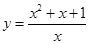 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用= )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
已知A=a+2,B=2a2-3a+10,C=a2+5a-3,
(1)求证:无论a为何值,A-B<0成立,并指出A,B的大小关系;
(2)请分析A与C的大小关系.
先阅读理解下面的例题,再按要求解答下列问题:
例题 :求代数式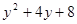 的最小值.
的最小值.
解: 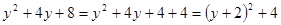
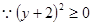

 的最小值是
的最小值是 .
.
(1)代数式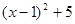 的最小值 ;
的最小值 ;
(2)求代数式 的最小值;
的最小值;
(3)某居民小区要在一块一边靠墙(墙长
 )的空地上建一个长方形花园
)的空地上建一个长方形花园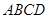 ,花园一边靠墙,另三边用总长为
,花园一边靠墙,另三边用总长为
 的栅栏围成.如图,设
的栅栏围成.如图,设 (
( ),请问:当
),请问:当 取何值时,花园的面积最大?最大面积是多少?
取何值时,花园的面积最大?最大面积是多少?
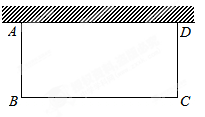
如图,利用一面墙(墙的长度为20米),用36米长的篱笆围成两个长方形鸡场,鸡场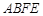 与鸡场
与鸡场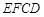 ,中间
,中间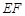 用一道篱笆隔开,每个鸡场均留一道1米宽的门,设
用一道篱笆隔开,每个鸡场均留一道1米宽的门,设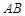 的长为
的长为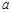
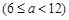 米.
米.
(1)当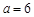 时,求点
时,求点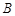 到点
到点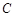 的距离;
的距离;
(2)用含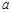 的代数式表示两个鸡场的面积和,并将所得式子化简;
的代数式表示两个鸡场的面积和,并将所得式子化简;
(3)两个鸡场的面积和有最大值吗?若有,请求出最大值;若没有,请说明理由.
试题篮
()