为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 |
乙种客车 |
|
载客量 (人 辆) |
30 |
42 |
租金 (元 辆) |
300 |
400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
某年5月,我国南方某省 、 两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市 、 获知 、 两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知 市有救灾物资240吨, 市有救灾物资260吨,现将这些救灾物资全部调往 、 两市.已知从 市运往 、 两市的费用分别为每吨20元和25元,从 市运往 、 两市的费用别为每吨15元和30元,设从 市运往 市的救灾物资为 吨.
(1)请填写下表
(吨) |
(吨) |
合计(吨) |
|
(吨) |
|
|
240 |
(吨) |
|
|
260 |
总计(吨) |
200 |
300 |
500 |
(2)设 、 两市的总运费为 元,求 与 之间的函数关系式,并写出自变量 的取值范围;
(3)经过抢修,从 市到 市的路况得到了改善,缩短了运输时间,运费每吨减少 元 ,其余路线运费不变.若 、 两市的总运费的最小值不小于10320元,求 的取值范围.
我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.例如,代数式 的几何意义是数轴上 所对应的点与2所对应的点之间的距离:因为 ,所以 的几何意义就是数轴上 所对应的点与 所对应的点之间的距离.
(1)发现问题:代数式 的最小值是多少?
(2)探究问题:如图,点 、 、 分别表示数 、2、 , .
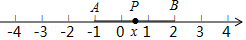
的几何意义是线段 与 的长度之和,
当点 在线段 上时, ,当点 在点 的左侧或点 的右侧时, .
的最小值是3.
(3)解决问题:
① 的最小值是 ;
②利用上述思想方法解不等式: ;
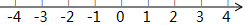
③当 为何值时,代数式 的最小值是2.
甲、乙两家商场平时以同样价格出售相同的商品.新冠疫情期间,为了减少库存,甲、乙两家商场打折促销.甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.
(1)以 (单位:元)表示商品原价, (单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数解析式;
(2)新冠疫情期间如何选择这两家商场去购物更省钱?
某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有 型和 型两种分类垃圾桶, 型分类垃圾桶500元 个, 型分类垃圾桶550元 个,总费用不超过3100元,则不同的购买方式有
A.2种B.3种C.4种D.5种
为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有 , 两种型号的健身器材可供选择.
(1)劲松公司2015年每套 型健身器材的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6万元,求每套 型健身器材年平均下降率 ;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司 , 两种型号的健身器材共80套,采购专项经费总计不超过112万元,采购合同规定:每套 型健身器材售价为1.6万元,每套 型健身器材售价为 万元.
① 型健身器材最多可购买多少套?
②安装完成后,若每套 型和 型健身器材一年的养护费分别是购买价的 和 ,市政府计划支出10万元进行养护,问该计划支出能否满足一年的养护需要?
某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工 个零件 为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知 的值至少为
A.10B.9C.8D.7
某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完,商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于 ,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
对一个实数 按如图所示的程序进行操作,规定:程序运行从“输入一个实数 ”到“结果是否大于88?”为一次操作.如果操作只进行一次就停止,则 的取值范围是 .

推进农村土地集约式管理,提高土地的使用效率是新农村建设的一项重要举措.某村在小城镇建设中集约了2400亩土地,计划对其进行平整.经投标,由甲乙两个工程队来完成平整任务.甲工程队每天可平整土地45亩,乙工程队每天可平整土地30亩.已知乙工程队每天的工程费比甲工程队少500元,当甲工程队所需工程费为12000元,乙工程队所需工程费为9000元时,两工程队工作天数刚好相同.
(1)甲乙两个工程队每天各需工程费多少元?
(2)现由甲乙两个工程队共同参与土地平整,已知两个工程队工作天数均为正整数,且所有土地刚好平整完,总费用不超过110000元.
①甲乙两工程队分别工作的天数共有多少种可能?
②写出其中费用最少的一种方案,并求出最低费用.
某书店现有资金7700元,计划全部用于购进甲、乙、丙三种图书共20套,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元.书店将甲、乙、丙三种图书的售价分别定为每套550元,430元,310元.设书店购进甲种图书 套,乙种图书 套,请解答下列问题:
(1)请求出 与 的函数关系式(不需要写出自变量的取值范围);
(2)若书店购进甲、乙两种图书均不少于1套,则该书店有几种进货方案?
(3)在(1)和(2)的条件下,根据市场调查,书店决定将三种图书的售价作如下调整:甲种图书的售价不变,乙种图书的售价上调 为正整数)元,丙种图书的售价下调 元,这样三种图书全部售出后,所获得的利润比(2)中某方案的利润多出20元,请直接写出书店是按哪种方案进的货及 的值.
春平中学要为学校科技活动小组提供实验器材,计划购买 型、 型两种型号的放大镜.若购买8个 型放大镜和5个 型放大镜需用220元;若购买4个 型放大镜和6个 型放大镜需用152元.
(1)求每个 型放大镜和每个 型放大镜各多少元;
(2)春平中学决定购买 型放大镜和 型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个 型放大镜?
某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.
(1)求购买1个排球、1个篮球的费用分别是多少元?
(2)若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?
某文具店最近有 , 两款毕业纪念册比较畅销,近两周的销售情况是:第一周 款销售数量是15本, 款销售数量是10本,销售总价是230元;第二周 款销售数量是20本, 款销售数量是10本,销售总价是280元.
(1)求 , 两款毕业纪念册的销售单价;
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本 款毕业纪念册.
试题篮
()