某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元.已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
(1)求甲、乙两种商品的每件进价;
(2)该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
小黄准备给长 ,宽 的长方形客厅铺设瓷砖,现将其划分成一个长方形 区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足 ,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元 ,面积为 ,区域Ⅱ的瓷砖均价为200元 ,且两区域的瓷砖总价为不超过12000元,求 的最大值;
(2)若区域Ⅰ满足 ,区域Ⅱ四周宽度相等
①求 , 的长;
②若甲、丙两瓷砖单价之和为300元 ,乙、丙瓷砖单价之比为 ,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.

2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度.
(1)求这个月晴天的天数.
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本(不计其它费用,结果取整数).

某商场销售 , 两种品牌的教学设备,这两种教学设备的进价和售价如表所示
|
|
|
进价(万元 套) |
1.5 |
1.2 |
售价(万元 套) |
1.65 |
1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进 , 两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少 种设备的购进数量,增加 种设备的购进数量,已知 种设备增加的数量是 种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问 种设备购进数量至多减少多少套?
为了美化市容市貌,政府决定将城区旁边一块162亩的荒地改建为湿地公园,规划公园分为绿化区和休闲区两部分.
(1)若休闲区面积是绿化区面积的 ,求改建后的绿化区和休闲区各有多少亩?
(2)经预算,绿化区的改建费用平均每亩35000元,休闲区的改建费用平均每亩25000元,政府计划投入资金不超过550万元,那么绿化区的面积最多可以达到多少亩?
攀枝花市出租车的收费标准是:起步价5元(即行驶距离不超过2千米都需付5元车费),超过2千米以后,每增加1千米,加收1.8元(不足1千米按1千米计).某同学从家乘出租车到学校,付了车费24.8元.求该同学的家到学校的距离在什么范围?
有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完.其中每辆大货车一次运货花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本乙图书?
某报刊销售处从报社购进甲、乙两种报纸进行销售.已知从报社购进甲种报纸200份与乙种报纸300份共需360元,购进甲种报纸300份与乙种报纸200份共需340元
(1)求购进甲、乙两种报纸的单价;
(2)已知销售处卖出甲、乙两种报纸的售价分别为每份1元、1.5元.销售处每天从报社购进甲、乙两种报纸共600份,若每天能全部销售完并且销售这两种报纸的总利润不低于300元,问该销售处每天最多购进甲种报纸多少份?
某车行去年 型车的销售总额为6万元,今年每辆车的售价比去年减少400元.若卖出的数量相同,销售总额将比去年减少 .
(1)求今年 型车每辆车的售价.
(2)该车行计划新进一批 型车和 型车共45辆,已知 、 型车的进货价格分别是1100元、1400元,今年 型车的销售价格是2000元,要求 型车的进货数量不超过 型车数量的两倍,应如何进货才能使这批车获得最大利润,最大利润是多少?
学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”.这批单车分为 , 两种不同款型,其中 型车单价400元, 型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放 , 两种款型的单车共100辆,总价值36800元.试问本次试点投放的 型车与 型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中 , 两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有 型车与 型车各多少辆?
我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.例如,代数式 的几何意义是数轴上 所对应的点与2所对应的点之间的距离:因为 ,所以 的几何意义就是数轴上 所对应的点与 所对应的点之间的距离.
(1)发现问题:代数式 的最小值是多少?
(2)探究问题:如图,点 、 、 分别表示数 、2、 , .
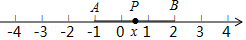
的几何意义是线段 与 的长度之和,
当点 在线段 上时, ,当点 在点 的左侧或点 的右侧时, .
的最小值是3.
(3)解决问题:
① 的最小值是 ;
②利用上述思想方法解不等式: ;
③当 为何值时,代数式 的最小值是2.
试题篮
()