初中数学分段函数试题

如图，在矩形 $\mathit{ABCD}$中， $\mathit{AB}=3\mathit{cm}$， $\mathit{AD}=\sqrt{3}\mathit{cm}$．动点 $P$从点 $A$出发沿折线 $\mathit{AB}-\mathit{BC}$向终点 $C$运动，在边 $\mathit{AB}$上以 $1\mathit{cm}/s$的速度运动；在边 $\mathit{BC}$上以 $\sqrt{3}\mathit{cm}/s$的速度运动，过点 $P$作线段 $\mathit{PQ}$与射线 $\mathit{DC}$相交于点 $Q$，且 $\angle \mathit{PQD}=60°$，连接 $\mathit{PD}$， $\mathit{BD}$．设点 $P$的运动时间为 $x\left(s\right)$， $\mathit{\Delta DPQ}$与 $\mathit{\Delta DBC}$重合部分图形的面积为 $y\left(c{m}^2\right)$．

（1）当点 $P$与点 $A$重合时，直接写出 $\mathit{DQ}$的长；

（2）当点 $P$在边 $\mathit{BC}$上运动时，直接写出 $\mathit{BP}$的长（用含 $x$的代数式表示）；

（3）求 $y$关于 $x$的函数解析式，并写出自变量 $x$的取值范围．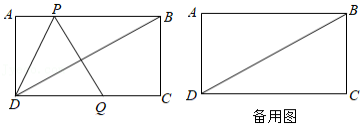

在"看图说故事"活动中，某学习小组结合图象设计了一个问题情境．已知学校、书店、陈列馆依次在同一条直线上，书店离学校 $12\mathit{km}$ ，陈列馆离学校 $20\mathit{km}$ ．李华从学校出发，匀速骑行 $0.6h$ 到达书店；在书店停留 $0.4h$ 后，匀速骑行 $0.5h$ 到达陈列馆；在陈列馆参观学习一段时间，然后回学校；回学校途中，匀速骑行 $0.5h$ 后减速，继续匀速骑行回到学校．给出的图象反映了这个过程中李华离学校的距离 $y\mathit{km}$ 与离开学校的时间 $xh$ 之间的对应关系．

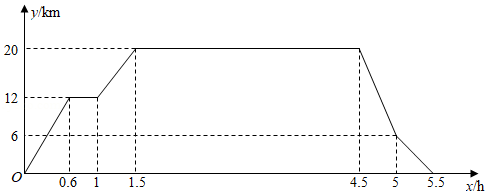
请根据相关信息，解答下列问题：

（Ⅰ）填表：

离开学校的时间     $/h$	0.1	0.5	0.8	1	3
离学校的距离     $/\mathit{km}$	2	10		12

（Ⅱ）填空：

①书店到陈列馆的距离为 　　 $\mathit{km}$ ；

②李华在陈列馆参观学习的时间为 　　 $h$ ；

③李华从陈列馆回学校途中，减速前的骑行速度为 　　 $\mathit{km}/h$ ；

④当李华离学校的距离为 $4\mathit{km}$ 时，他离开学校的时间为 　　 $h$ ．

（Ⅲ）当 $0⩽x⩽1.5$ 时，请直接写出 $y$ 关于 $x$ 的函数解析式．

为了节能减排，鼓励居民节约用电，某市出台了新的居民用电收费标准：（1）若每户居民每月用电量不超过100度，则按0.60元 $/$度计算；（2）若每户居民每月用电量超过100度，则超过部分按0.8元 $/$度计算（未超过部分仍按每度电0.60元 $/$度计算），现假设某户居民某月用电量是 $x$（单位：度），电费为 $y$（单位：元），则 $y$与 $x$的函数关系用图象表示正确的是 $($　　 $)$

A．B．

C．D．

某景点试开放期间，团队收费方案如下：不超过30人时，人均收费120元；超过30人且不超过 $m(30<m⩽100)$人时，每增加1人，人均收费降低1元；超过 $m$人时，人均收费都按照 $m$人时的标准．设景点接待有 $x$名游客的某团队，收取总费用为 $y$元．

（1）求 $y$关于 $x$的函数表达式；

（2）景点工作人员发现：当接待某团队人数超过一定数量时，会出现随着人数的增加收取的总费用反而减少这一现象．为了让收取的总费用随着团队中人数的增加而增加，求 $m$的取值范围．

已知函数 $y=\left\{\begin{array}{c}-x+1(x<2)\\ -\frac{2}{x}(x⩾2)\end{array}\right.$，当函数值为3时，自变量 $x$的值为 $($　　 $)$

A． $-2$B． $-\frac{2}{3}$C． $-2$或 $-\frac{2}{3}$D． $-2$或 $-\frac{3}{2}$

如图，在四边形 $\mathit{ABCD}$ 中， $\mathit{AD}//\mathit{BC}$ ， $\angle A=45°$ ， $\angle C=90°$ ， $\mathit{AD}=4\mathit{cm}$ ， $\mathit{CD}=3\mathit{cm}$ ．动点 $M$ ， $N$ 同时从点 $A$ 出发，点 $M$ 以 $\sqrt{2}\mathit{cm}/s$ 的速度沿 $\mathit{AB}$ 向终点 $B$ 运动，点 $N$ 以 $2\mathit{cm}/s$ 的速度沿折线 $\mathit{AD}-\mathit{DC}$ 向终点 $C$ 运动．设点 $N$ 的运动时间为 $\mathit{ts}$ ， $\mathit{\Delta AMN}$ 的面积为 $\mathit{Sc}{m}^2$ ，则下列图象能大致反映 $S$ 与 $t$ 之间函数关系的是 $($ 　　 $)$

A．		B．
C．		D．

今年是“精准扶贫”攻坚关键年，某扶贫工作队为对口扶贫村引进建立了一村集体企业，并无偿提供一笔无息贷款作为启动资金，双方约定：①企业生产出的产品全部由扶贫工作队及时联系商家收购；②企业从生产销售的利润中，要保证按时发放工人每月最低工资32000元．已知该企业生产的产品成本为20元 $/$件，月生产量 $y$（千件）与出厂价 $x$（元 $\left)\right(25⩽x⩽50)$的函数关系可用图中的线段 $\mathit{AB}$和 $\mathit{BC}$表示，其中 $\mathit{AB}$的解析式为 $y=-\frac{1}{20}x+m(m$为常数）．

（1）求该企业月生产量 $y$（千件）与出厂价 $x$（元 $)$之间的函数关系式，并写出自变量 $x$的取值范围．

（2）当该企业生产出的产品出厂价定为多少元时，月利润 $W$（元 $)$最大？最大利润是多少？ $[$月利润 $=$（出厂价 $-$成本） $\times$月生产量 $-$工人月最低工资 $]$．

已知函数 $y=\left\{\begin{array}{c}\frac{3}{x},x⩽-1,\\ 3x,-1<x⩽1,\\ \frac{3}{x},x⩾1\cdot \end{array}\right.$

（1）画出函数图象；

列表：

$x$	$\dots$	$-3$								$\dots$
$y$	$\dots$									$.\dots$

描点，连线得到函数图象：

（2）该函数是否有最大或最小值？若有，求出其值，若没有，简述理由；

（3）设 $(x_1$， $y_1)$， $(x_2$， $y_2)$是函数图象上的点，若 $x_1+x_2=0$，证明： $y_1+y_2=0$．

对于实数a，b，我们定义符号 $\mathit{max}\left\{a，b\right\}$的意义为：当 $a\ge b$时， $\mathit{max}\left\{a，b\right\}＝a$；当 $a＜b$时， $\mathit{max}\left\{a，b\right\}＝b$；如： $\mathit{max}\left\{4\mathit{，﹣}2\right\}＝4$， $\mathit{max}\{3,3\}＝3$，若关于x的函数为 $y＝\mathit{max}\{x+3\mathit{，﹣}x+1\}$，则该函数的最小值是（　　）

A．0B．2C．3D．4

某周日上午 $8:00$小宇从家出发，乘车1小时到达某活动中心参加实践活动． $11:00$时他在活动中心接到爸爸的电话，因急事要求他在 $12:00$前回到家，他即刻按照来活动中心时的路线，以5千米 $/$小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家 $x$（小时）后，到达离家 $y$（千米）的地方，图中折线 $\mathit{OABCD}$表示 $y$与 $x$之间的函数关系．

（1）活动中心与小宇家相距　   　千米，小宇在活动中心活动时间为　 　小时，他从活动中心返家时，步行用了　    　小时；

（2）求线段 $\mathit{BC}$所表示的 $y$（千米）与 $x$（小时）之间的函数关系式（不必写出 $x$所表示的范围）；

（3）根据上述情况（不考虑其他因素），请判断小宇是否能在 $12:00$前回到家，并说明理由．

如图，在等腰直角三角形中，，，于点，点从点出发，沿方向以的速度运动到点停止，在运动过程中，过点作交于点，以线段为边作等腰直角三角形，且（点，位于异侧）．设点的运动时间为，与重叠部分的面积为

（1）当点落在上时，　　；

（2）当点落在上时，　　；

（3）求关于的函数解析式，并写出自变量的取值范围．

甲、乙两个批发店销售同一种苹果，在甲批发店，不论一次购买数量是多少，价格均为6元．在乙批发店，一次购买数量不超过时，价格为7元；一次购买数量超过时，其中有的价格仍为7元，超过部分的价格为5元．设小王在同一个批发店一次购买苹果的数量为．

（Ⅰ）根据题意填表：

一次购买数量	30	50	150
甲批发店花费元		300
乙批发店花费元		350

（Ⅱ）设在甲批发店花费元，在乙批发店花费元，分别求，关于的函数解析式；

（Ⅲ）根据题意填空：

①若小王在甲批发店和在乙批发店一次购买苹果的数量相同，且花费相同，则他在同一个批发店一次购买苹果的数量为　　；

②若小王在同一个批发店一次购买苹果的数量为，则他在甲、乙两个批发店中的　　批发店购买花费少；

③若小王在同一个批发店一次购买苹果花费了360元，则他在甲、乙两个批发店中的　　批发店购买数量多．

已知函数的图象如图所示，若直线与该图象恰有三个不同的交点，则的取值范围为　　．

小强的爸爸从家骑自行车去图书馆借书，途中遇到了从图书馆步行回家的小强，爸爸借完书后迅速回家，途中追上了小强，便用自行车载上小强一起回家，结果爸爸比自己单独骑车回家晚到1分钟，两人与家的距离 $S$（千米）和爸爸从家出发后的时间 $t$（分钟）之间的关系如图所示．

（1）图书馆离家有多少千米？

（2）爸爸和小强第一次相遇时，离家多少千米？

（3）爸爸载上小强后一起回家的速度是多少？

在初中阶段的函数学习中，我们经历了“确定函数的表达式利用函数图象研究其性质一一运用函数解决问题“的学习过程．在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象．同时，我们也学习了绝对值的意义．

结合上面经历的学习过程，现在来解决下面的问题在函数中，当时，；当时，．

（1）求这个函数的表达式；

（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质；

（3）已知函的图象如图所示，结合你所画的函数图象，直接写出不等式的解集．