某物流公司引进、
两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,
种机器人于某日0时开始搬运,过了1小时,
种机器人也开始搬运,如图,线段
表示
种机器人的搬运量
(千克)与时间
(时
的函数图象,线段
表示
种机器人的搬运量
(千克)与时间
(时
的函数图象.根据图象提供的信息,解答下列问题:
(1)求关于
的函数解析式;
(2)如果、
两种机器人连续搬运5个小时,那么
种机器人比
种机器人多搬运了多少千克?

设 、 是任意两个实数,用 , 表示 、 两数中较大者,例如: , , , , , ,参照上面的材料,解答下列问题:
(1) , , , ;
(2)若 , ,求 的取值范围;
(3)求函数 与 的图象的交点坐标,函数 的图象如图所示,请你在图中作出函数 的图象,并根据图象直接写出 , 的最小值.

设一次函数 的图象经过点 ,且 的值随 的值增大而增大,则该一次函数的图象一定不经过
| A. |
第一象限 |
B. |
第二象限 |
C. |
第三象限 |
D. |
第四象限 |
如图,直线 与 轴, 轴分别交于 、 两点, 与△ 是以点 为位似中心的位似图形,且相似比为 ,则点 的坐标为 .

已知等腰三角形的周长是10,底边长 是腰长 的函数,则下列图象中,能正确反映 与 之间函数关系的图象是
A.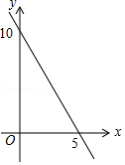 B.
B.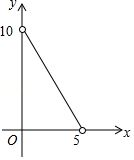
C. D.
D.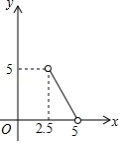
(年青海省中考)已知一次函数 与反比例函数
与反比例函数 ,那么它们在同一坐标系中的图象可能是( )
,那么它们在同一坐标系中的图象可能是( )
A. |
B. |
C. |
D. |
探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括函数性质的过程.以下是我们研究函数 性质及其应用的部分过程,请按要求完成下列各小题.
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
6 |
5 |
4 |
|
2 |
1 |
|
7 |
|
(1)写出函数关系式中 及表格中 , 的值:
, , ;
(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象,并根据图象写出该函数的一条性质: ;
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.
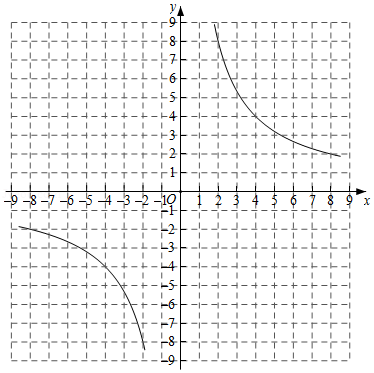
)已知正比例函数 与反比例函数 的图象都经过点 .
(1)求 , 的值;
(2)在图中画出正比例函数 的图象,并根据图象,写出正比例函数值大于反比例函数值时 的取值范围.
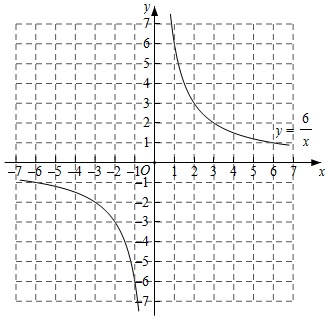
小慧根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数 的自变量 的取值范围是 ;
(2)列表,找出 与 的几组对应值.
|
|
|
0 |
1 |
2 |
3 |
|
|
|
b |
1 |
0 |
1 |
2 |
|
其中, ;
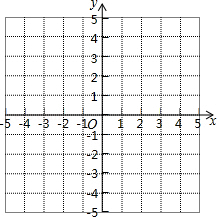
(3)在平面直角坐标系 中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .
试题篮
()