数形结合是解决数学问题常用的思想方法.如图,直线 与直线 相交于点 .根据图象可知,关于 的不等式 的解集是
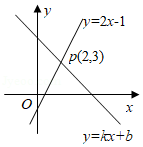
| A. |
|
B. |
|
C. |
|
D. |
|
如图①是甲,乙两个圆柱形水槽的横截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度 与注水时间 之间的关系如图②所示,根据图象解答下列问题:
(1)图②中折线 表示 槽中水的深度与注入时间之间的关系;线段 表示 槽中水的深度与注入时间之间的关系;铁块的高度为 .
(2)注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)

数形结合是解决数学问题常用的思想方法.如图,直线 和直线 相交于点 ,根据图象可知,方程 的解是
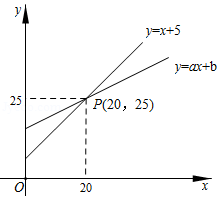
A. B. C. D.
如图,在平面直角坐标系中,直线 与直线 相交于点 ,并分别与 轴相交于点 、 .
(1)求交点 的坐标;
(2)求 的面积;
(3)请把图象中直线 在直线 上方的部分描黑加粗,并写出此时自变量 的取值范围.
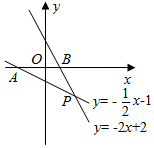
在平面直角坐标系中, 为坐标原点.若直线 分别与 轴、直线 交于点 、 ,则 的面积为
A.2B.3C.4D.6
如图,在平面直角坐标系中,一次函数 的图象经过点 ,且与 轴相交于点 ,与正比例函数 的图象相交于点 ,点 的横坐标为1.
(1)求 、 的值;
(2)若点 在 轴负半轴上,且满足 ,求点 的坐标.

如图,直线 与直线 相交于点 .
(1)求 , 的值;
(2)垂直于 轴的直线 与直线 , 分别交于点 , ,若线段 长为2,求 的值.

如图,已知函数 和 图象交于点 ,当 时,根据图象可得 的取值范围是
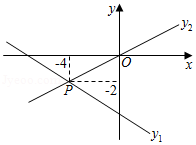
A. B. C. D.
对于实数 , ,定义符号 , ,其意义为:当 时, , ;当 时, , .例如: , ,若关于 的函数 , ,则该函数的最大值为
A. B.1C. D.
试题篮
()