初中数学一次函数的应用解答题

新冠疫情期间，口罩成为了人们出行必备的防护工具．某药店三月份共销售 $A$， $B$两种型号的口罩9000只，共获利润5000元，其中 $A$， $B$两种型号口罩所获利润之比为 $2:3$．已知每只 $B$型口罩的销售利润是 $A$型口罩的1.2倍．

（1）求每只 $A$型口罩和 $B$型口罩的销售利润；

（2）该药店四月份计划一次性购进两种型号的口罩共10000只，其中 $B$型口罩的进货量不超过 $A$型口罩的1.5倍，设购进 $A$型口罩 $m$只，这10000只口罩的销售总利润为 $W$元．该药店如何进货，才能使销售总利润最大？

宏兴企业接到一批产品的生产任务，按要求必须在14天内完成．已知每件产品的出厂价为60元．工人甲第 $x$天生产的产品数量为 $y$件， $y$与 $x$满足如下关系： $y=\left\{\begin{array}{c}7.5x(0⩽x⩽4)\\ 5x+10(4<x⩽14)\end{array}\right.$．

（1）工人甲第几天生产的产品数量为70件？

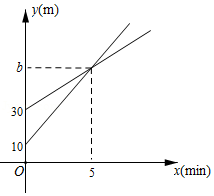
（2）设第 $x$天生产的产品成本为 $P$元 $/$件， $P$与 $x$的函数图象如图．工人甲第 $x$天创造的利润为 $W$元，求 $W$与 $x$的函数关系式，并求出第几天时，利润最大，最大利润是多少？

某种型号汽车油箱容量为 $40L$，每行驶 $100\mathit{km}$耗油 $10L$．设一辆加满油的该型号汽车行驶路程为 $x\left(\mathit{km}\right)$，行驶过程中油箱内剩余油量为 $y\left(L\right)$．

（1）求 $y$与 $x$之间的函数表达式；

（2）为了有效延长汽车使用寿命，厂家建议每次加油时油箱内剩余油量不低于油箱容量的 $\frac{1}{4}$，按此建议，求该辆汽车最多行驶的路程．

小明放学后从学校回家，出发5分钟时，同桌小强发现小明的数学作业卷忘记拿了，立即拿着数学作业卷按照同样的路线去追赶小明，小强出发10分钟时，小明才想起没拿数学作业卷，马上以原速原路返回，在途中与小强相遇．两人离学校的路程 $y$（米 $)$与小强所用时间 $x$（分钟）之间的函数图象如图所示．

（1）求函数图象中 $a$的值；

（2）求小强的速度；

（3）求线段 $\mathit{AB}$的函数解析式，并写出自变量的取值范围．

渠县是全国优质黄花主产地，某加工厂加工黄花的成本为30元 $/$千克，根据市场调查发现，批发价定为48元 $/$千克时，每天可销售500千克，为增大市场占有率，在保证盈利的情况下，工厂采取降价措施，批发价每千克降低1元，每天销量可增加50千克．

（1）写出工厂每天的利润 $W$元与降价 $x$元之间的函数关系．当降价2元时，工厂每天的利润为多少元？

（2）当降价多少元时，工厂每天的利润最大，最大为多少元？

（3）若工厂每天的利润要达到9750元，并让利于民，则定价应为多少元？

小明匀速跑步从甲地到乙地，在途中因故停留了一段时间后，仍按原速跑步，小强骑自行车比小明晚出发一段时间，以400米 $/$分的速度匀速从乙地到甲地，两人距离乙地的路程 $y$（米 $)$与小明出发后所用时间 $t$（分钟）之间的函数图象如图所示，

（1）求小明跑步的速度；

（2）求小明停留结束后 $y$与 $x$之间的函数解析式，并写出自变量的取值范围；

（3）求小明与小强相遇时 $x$的值．

某村在推进美丽乡村活动中，决定建设幸福广场，计划铺设相同大小规格的红色和蓝色地砖．经过调查．获取信息如下：

	购买数量低于5000块	购买数量不低于5000块
红色地砖	原价销售	以八折销售
蓝色地砖	原价销售	以九折销售

如果购买红色地砖4000块，蓝色地砖6000块，需付款86000元；如果购买红色地砖10000块，蓝色地砖3500块，需付款99000元．

（1）红色地砖与蓝色地砖的单价各多少元？

（2）经过测算，需要购置地砖12000块，其中蓝色地砖的数量不少于红色地砖的一半，并且不超过6000块，如何购买付款最少？请说明理由．

为了落实党的“精准扶贫”政策， $A$、 $B$两城决定向 $C$、 $D$两乡运送肥料以支持农村生产，已知 $A$、 $B$两城共有肥料500吨，其中 $A$城肥料比 $B$城少100吨，从 $A$城往 $C$、 $D$两乡运肥料的费用分别为20元 $/$吨和25元 $/$吨；从 $B$城往 $C$、 $D$两乡运肥料的费用分别为15元 $/$吨和24元 $/$吨．现 $C$乡需要肥料240吨， $D$乡需要肥料260吨．

（1） $A$城和 $B$城各有多少吨肥料？

（2）设从 $A$城运往 $C$乡肥料 $x$吨，总运费为 $y$元，求出最少总运费．

（3）由于更换车型，使 $A$城运往 $C$乡的运费每吨减少 $a(0<a<6)$元，这时怎样调运才能使总运费最少？

2020年初，新冠肺炎疫情爆发，市场上防疫口罩热销，某医药公司每月生产甲、乙两种型号的防疫口罩共20万只，且所有口罩当月全部售出，其中成本、售价如下表：

型号 价格（元 $/$ 只） 项目	甲	乙
成本	12	4
售价	18	6

（1）若该公司三月份的销售收入为300万元，求生产甲、乙两种型号的防疫口罩分别是多少万只？

（2）如果公司四月份投入成本不超过216万元，应怎样安排甲、乙两种型号防疫口罩的产量，可使该月公司所获利润最大？并求出最大利润．

Ⅰ号无人机从海拔 $10m$ 处出发，以 $10m/\mathit{min}$ 的速度匀速上升，Ⅱ号无人机从海拔 $30m$ 处同时出发，以 $a(m/\mathit{min})$ 的速度匀速上升，经过 $5\mathit{min}$ 两架无人机位于同一海拔高度 $b\left(m\right)$ ．无人机海拔高度 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 的关系如图．两架无人机都上升了 $15\mathit{min}$ ．

（1）求 $b$ 的值及Ⅱ号无人机海拔高度 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 的关系式；

（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高28米．

李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程 $s$ （千米）与行驶时间 $t$ （小时）的关系如图所示（中途休息、加油的时间不计）．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升 $/$ 千米，请根据图象解答下列问题：

（1）写出工厂离目的地的路程；

（2）求 $s$ 关于 $t$ 的函数表达式；

（3）当货车显示加油提醒后，问行驶时间 $t$ 在怎样的范围内货车应进站加油？

国庆节前，某超市为了满足人们的购物需求，计划购进甲、乙两种水果进行销售．经了解，甲种水果和乙种水果的进价与售价如下表所示．

	甲	乙
进价（元/千克）	x	x+4
售价（元/千克）	20	25

已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同．

（1）求x的值；

（2）若超市购进这两种水果共100千克，其中甲种水果的重量不低于乙种水果重量的3倍，则超市应如何进货才能获得最大利润，最大利润是多少？

疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 $a$ 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数 $y$ （万人）与各自接种时间 $x$ （天 $)$ 之间的关系如图所示．

（1）直接写出乙地每天接种的人数及 $a$ 的值；

（2）当甲地接种速度放缓后，求 $y$ 关于 $x$ 的函数解析式，并写出自变量 $x$ 的取值范围；

（3）当乙地完成接种任务时，求甲地未接种疫苗的人数．

某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术．这种瓜苗早期在农科所的温室中生长，长到大约 $20\mathit{cm}$时，移至该村的大棚内，沿插杆继续向上生长．研究表明，60天内，这种瓜苗生长的高度 $y\left(\mathit{cm}\right)$与生长时间 $x$（天 $)$之间的关系大致如图所示．

（1）求 $y$与 $x$之间的函数关系式；

（2）当这种瓜苗长到大约 $80\mathit{cm}$时，开始开花结果，试求这种瓜苗移至大棚后．继续生长大约多少天，开始开花结果？

某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品 $x$（吨），生产甲、乙两种产品获得的总利润为 $y$（万元）．

（1）求 $y$与 $x$之间的函数表达式；

（2）若每生产1吨甲产品需要 $A$原料0.25吨，每生产1吨乙产品需要 $A$原料0.5吨．受市场影响，该厂能获得的 $A$原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．