已知 、 两地相距 ,一辆货车从 前往 地,途中因装载货物停留一段时间.一辆轿车沿同一条公路从 地前往 地,到达 地后(在 地停留时间不计)立即原路原速返回.如图是两车距 地的距离 与货车行驶时间 之间的函数图象,结合图象回答下列问题:
(1)图中 的值是 ;轿车的速度是 ;
(2)求货车从 地前往 地的过程中,货车距 地的距离 与行驶时间 之间的函数关系式;
(3)直接写出轿车从 地到 地行驶过程中,轿车出发多长时间与货车相距 ?

“互联网 ”让我国经济更具活力,直播助销就是运用“互联网 ”的生机勃勃的销售方式,让大山深处的农产品远销全国各地.甲为当地特色花生与茶叶两种产品助销.已知每千克花生的售价比每千克茶叶的售价低40元,销售50千克花生与销售10千克茶叶的总售价相同.
(1)求每千克花生、茶叶的售价;
(2)已知花生的成本为6元 千克,茶叶的成本为36元 千克,甲计划两种产品共助销60千克,总成本不高于1260元,且花生的数量不高于茶叶数量的2倍.则花生、茶叶各销售多少千克可获得最大利润?最大利润是多少?
小刚和小亮两人沿着直线跑道都从甲地出发,沿着同一方向到达乙地,甲乙两地之间的距离是720米,先到乙地的人原地休息.已知小刚先从甲地出发4秒后,小亮从甲地出发,两人均保持匀速前行第一次相遇后,保持原速跑一段时间,小刚突然加速,速度比原来增加了2米 秒,并保持这一速度跑到乙地(小刚加速过程忽略不计).小刚与小亮两人的距离 (米 与小亮出发时间 (秒 之间的函数图象,如图所示.根据所给信息解决以下问题.
(1) , ;
(2)求 和 所在直线的解析式;
(3)直接写出 为何值时,两人相距30米.

如图①是甲,乙两个圆柱形水槽的横截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度 与注水时间 之间的关系如图②所示,根据图象解答下列问题:
(1)图②中折线 表示 槽中水的深度与注入时间之间的关系;线段 表示 槽中水的深度与注入时间之间的关系;铁块的高度为 .
(2)注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)

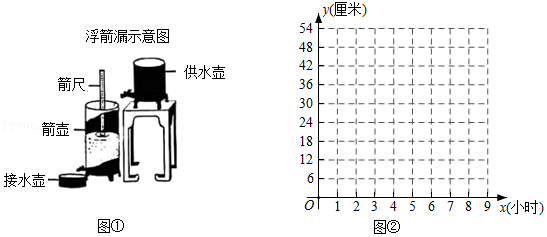
《九章算术》中记载,浮箭漏(图① 出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间.某学校 小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
【实验观察】实验小组通过观察,每2小时记录一次箭尺读数,得到如表:
供水时间 (小时) |
0 |
2 |
4 |
6 |
8 |
箭尺读数 (厘米) |
6 |
18 |
30 |
42 |
54 |
【探索发现】①建立平面直角坐标系,如图②,横轴表示供水时间 .纵轴表示箭尺读数 ,描出以表格中数据为坐标的各点.
②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
【结论应用】应用上述发现的规律估算:
①供水时间达到12小时时,箭尺的读数为多少厘米?
②如果本次实验记录的开始时间是上午 ,那当箭尺读数为90厘米时是几点钟?(箭尺最大读数为100厘米)
黔东南州某销售公司准备购进 、 两种商品,已知购进3件 商品和2件 商品,需要1100元;购进5件 商品和3件 商品,需要1750元.
(1)求 、 两种商品的进货单价分别是多少元?
(2)若该公司购进 商品200件, 商品300件,准备把这些商品全部运往甲、乙两地销售.已知每件 商品运往甲、乙两地的运费分别为20元和25元;每件 商品运往甲、乙两地的运费分别为15元和24元.若运往甲地的商品共240件,运往乙地的商品共260件.
①设运往甲地的 商品为 (件 ,投资总运费为 (元 ,请写出 与 的函数关系式;
②怎样调运 、 两种商品可使投资总费用最少?最少费用是多少元?(投资总费用 购进商品的费用 运费)
为了实施乡村振兴战略,帮助农民增加收入,市政府大力扶持农户发展种植业,每亩土地每年发放种植补贴120元.张远村老张计划明年承租部分土地种植某种经济作物.考虑各种因素,预计明年每亩土地种植该作物的成本 (元 与种植面积 (亩 之间满足一次函数关系,且当 时, ;当 时, .
(1)求 与 之间的函数关系式(不求自变量的取值范围);
(2)受区域位置的限制,老张承租土地的面积不得超过240亩.若老张明年销售该作物每亩的销售额能达到2160元,当种植面积为多少时,老张明年种植该作物的总利润最大?最大利润是多少?
(每亩种植利润 每亩销售额 每亩种植成本 每亩种植补贴)
如图1,小刚家、学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离 与他所用的时间 的函数关系如图2所示.
(1)小刚家与学校的距离为 ,小刚骑自行车的速度为 ;
(2)求小刚从图书馆返回家的过程中, 与 的函数表达式;
(3)小刚出发35分钟时,他离家有多远?

如图是一种单肩包,其背带由双层部分、单层部分和调节扣构成.小文购买时,售货员演示通过调节扣加长或缩短单层部分的长度,可以使背带的长度(单层部分与双层部分长度的和,其中调节扣所占长度忽略不计)加长或缩短,设双层部分的长度为 ,单层部分的长度为 .经测量,得到表中数据.
双层部分长度 |
2 |
8 |
14 |
20 |
单层部分长度 |
148 |
136 |
124 |
112 |
(1)根据表中数据规律,求出 与 的函数关系式;
(2)按小文的身高和习惯,背带的长度调为 时为最佳背带长.请计算此时双层部分的长度;
(3)设背带长度为 ,求 的取值范围.

甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元 ,如果一次购买 以上的苹果,超过 的部分按标价6折售卖.
(单位: 表示购买苹果的重量, (单位:元)表示付款金额.
(1)文文购买 苹果需付款 元;购买 苹果需付款 元;
(2)求付款金额 关于购买苹果的重量 的函数解析式;
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元 ,且全部按标价的8折售卖,文文如果要购买 苹果,请问她在哪个超市购买更划算?
为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如表所示:
品种 |
进价(元 斤) |
售价(元 斤) |
|
鲢鱼 |
|
5 |
|
草鱼 |
|
销量不超过200斤的部分 |
销量超过200斤的部分 |
8 |
7 |
||
已知老李购进10斤鲢鱼和20斤草鱼需要155元,购进20斤鲢鱼和10斤草鱼需要130元.
(1)求 , 的值;
(2)老李每天购进两种鱼共300斤,并在当天都销售完,其中销售鲢鱼不少于80斤且不超过120斤,设每天销售鲢鱼 斤(销售过程中损耗不计).
①分别求出每天销售鲢鱼获利 (元 ,销售草鱼获利 (元 与 的函数关系式,并写出 的取值范围;
②端午节这天,老李让利销售,将鲢鱼售价每斤降低 元,草鱼售价全部定为7元 斤,为了保证当天销售这两种鱼总获利 (元 最小值不少于320元,求 的最大值.
某公司经营某种农产品,零售一箱该农产品的利润是70元,批发一箱该农产品的利润是40元.
(1)已知该公司某月卖出100箱这种农产品共获利润4600元,问:该公司当月零售、批发这种农产品的箱数分别是多少?
(2)经营性质规定,该公司零售的数量不能多于总数量的 .现该公司要经营1000箱这种农产品,问:应如何规划零售和批发的数量,才能使总利润最大?最大总利润是多少?
为了做好防疫工作,学校准备购进一批消毒液.已知2瓶 型消毒液和3瓶 型消毒液共需41元,5瓶 型消毒液和2瓶 型消毒液共需53元.
(1)这两种消毒液的单价各是多少元?
(2)学校准备购进这两种消毒液共90瓶,且 型消毒液的数量不少于 型消毒液数量的 ,请设计出最省钱的购买方案,并求出最少费用.
某网店销售一款市场上畅销的蒸蛋器,进价为每个40元,在销售过程中发现,这款蒸蛋器销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为 元,每星期销售量为 个.
(1)请直接写出 (个 与 (元 之间的函数关系式;
(2)当销售单价是多少元时,该网店每星期的销售利润是2400元?
(3)当销售单价是多少元时,该网店每星期的销售利润最大?最大利润是多少元?
试题篮
()