初中数学一次函数的应用试题

在甲、乙两城市之间有一服务区，一辆客车从甲地驶往乙地，一辆货车从乙地驶往甲地．两车同时出发，匀速行驶，客车、货车离服务区的距离 $y_1$（千米）， $y_2$（千米）与行驶的时间 $x$（小时）的函数关系图象如图1所示．

（1）甲、乙两地相距　　千米．

（2）求出发3小时后，货车离服务区的路程 $y_2$（千米）与行驶时间 $x$（小时）之间的函数关系式．

（3）在客车和货车出发的同时，有一辆邮政车从服务区匀速去甲地取货后返回乙地（取货的时间忽略不计），邮政车离服务区的距离 $y_3$（千米）与行驶时间 $x$（小时）之间的函数关系图线如图2中的虚线所示，直接写出在行驶的过程中，经过多长时间邮政车与客车和货车的距离相等？

如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点 $A$．甲从中山路上点 $B$出发，骑车向北匀速直行；与此同时，乙从点 $A$出发，沿北京路步行向东匀速直行．设出发 $\mathit{xmin}$时，甲、乙两人与点 $A$的距离分别为 $y_{1}m$、 $y_{2}m$．已知 $y_1$、 $y_2$与 $x$之间的函数关系如图②所示．

（1）求甲、乙两人的速度；

（2）当 $x$取何值时，甲、乙两人之间的距离最短？

下列图象中，能反映等腰三角形顶角 $y$（度 $)$与底角 $x$（度 $)$之间的函数关系的是 $($　　 $)$

A．B．

C．D．

众志成城抗疫情，全国人民在行动．某公司决定安排大、小货车共20辆，运送260吨物资到 $A$地和 $B$地，支援当地抗击疫情．每辆大货车装15吨物资，每辆小货车装10吨物资，这20辆货车恰好装完这批物资．已知这两种货车的运费如下表：

目的地 车型	$A$地（元 $/$辆）	$B$地（元 $/$辆）
大货车	900	1000
小货车	500	700

现安排上述装好物资的20辆货车（每辆大货车装15吨物资，每辆小货车装10吨物资）中的10辆前往 $A$地，其余前往 $B$地，设前往 $A$地的大货车有 $x$辆，这20辆货车的总运费为 $y$元．

（1）这20辆货车中，大货车、小货车各有多少辆？

（2）求 $y$与 $x$的函数解析式，并直接写出 $x$的取值范围；

（3）若运往 $A$地的物资不少于140吨，求总运费 $y$的最小值．

我市从2018年1月1日开始，禁止燃油助力车上路，于是电动自行车的市场需求量日渐增多．某商店计划最多投入8万元购进 $A$、 $B$两种型号的电动自行车共30辆，其中每辆 $B$型电动自行车比每辆 $A$型电动自行车多500元．用5万元购进的 $A$型电动自行车与用6万元购进的 $B$型电动自行车数量一样．

（1）求 $A$、 $B$两种型号电动自行车的进货单价；

（2）若 $A$型电动自行车每辆售价为2800元， $B$型电动自行车每辆售价为3500元，设该商店计划购进 $A$型电动自行车 $m$辆，两种型号的电动自行车全部销售后可获利润 $y$元．写出 $y$与 $m$之间的函数关系式；

（3）在（2）的条件下，该商店如何进货才能获得最大利润？此时最大利润是多少元？

某校计划采购凳子，商场有 $A$、 $B$两种型号的凳子出售，并规定：对于 $A$型凳子，采购数量若超过250张，则超出部分可在原价基础上每张优惠 $a$元； $B$型凳子的售价为40元 $/$张．学校经测算，若购买300张 $A$型凳子需要花费14250元；若购买500张 $A$型凳子需要花费21250元．

（1）求 $a$的值；

（2）学校要采购 $A$、 $B$两种型号凳子共900张，且购买 $A$型凳子不少于150张且不超过 $B$型凳子数量的2倍，请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少？最少是多少元？

已知 $A$、 $B$两地相距3千米，小黄从 $A$地到 $B$地，平均速度为4千米 $/$小时，若用 $x$表示行走的时间（小时）， $y$表示余下的路程（千米），则 $y$关于 $x$的函数解析式是 $($　　 $)$

A． $y=4x(x⩾0)$B． $y=4x-3(x⩾\frac{3}{4})$

C． $y=3-4x(x⩾0)$D． $y=3-4x(0⩽x⩽\frac{3}{4})$

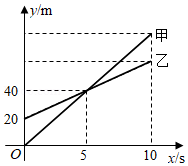
甲无人机从地面起飞，乙无人机从距离地面 $20m$ 高的楼顶起飞，两架无人机同时匀速上升 $10s$ ．甲、乙两架无人机所在的位置距离地面的高度 $y$ （单位： $m)$ 与无人机上升的时间 $x$ （单位： $s)$ 之间的关系如图所示．下列说法正确的是 $($ 　　 $)$

A．	$5s$ 时，两架无人机都上升了 $40m$
B．	$10s$ 时，两架无人机的高度差为 $20m$
C．	乙无人机上升的速度为 $8m/s$
D．	$10s$ 时，甲无人机距离地面的高度是 $60m$

某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品 $x$（吨），生产甲、乙两种产品获得的总利润为 $y$（万元）．

（1）求 $y$与 $x$之间的函数表达式；

（2）若每生产1吨甲产品需要 $A$原料0.25吨，每生产1吨乙产品需要 $A$原料0.5吨．受市场影响，该厂能获得的 $A$原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．

小明从家步行到学校需走的路程为1800米．图中的折线 $\mathit{OAB}$反映了小明从家步行到学校所走的路程 $s$（米 $)$与时间 $t$（分钟）的函数关系，根据图象提供的信息，当小明从家出发去学校步行15分钟时，到学校还需步行　　米．

快车从甲地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶，途中快车休息1.5小时，慢车没有休息．设慢车行驶的时间为 $x$小时，快车行驶的路程为 $y_1$千米，慢车行驶的路程为 $y_2$千米．如图中折线 $\mathit{OAEC}$表示 $y_1$与 $x$之间的函数关系，线段 $\mathit{OD}$表示 $y_2$与 $x$之间的函数关系．

请解答下列问题：

（1）求快车和慢车的速度；

（2）求图中线段 $\mathit{EC}$所表示的 $y_1$与 $x$之间的函数表达式；

（3）线段 $\mathit{OD}$与线段 $\mathit{EC}$相交于点 $F$，直接写出点 $F$的坐标，并解释点 $F$的实际意义．

某水果店以每千克8元的价格购进苹果若干千克，销售了部分苹果后，余下的苹果每千克降价4元销售，全部售完．销售金额 $y$（元 $)$与销售量 $x$（千克）之间的关系如图所示，请根据图象提供的信息完成下列问题：

（1）降价前苹果的销售单价是　     　元 $/$千克；

（2）求降价后销售金额 $y$（元 $)$与销售量 $x$（千克）之间的函数解析式，并写出自变量的取值范围；

（3）该水果店这次销售苹果盈利了多少元？

某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术．这种瓜苗早期在农科所的温室中生长，长到大约 $20\mathit{cm}$时，移至该村的大棚内，沿插杆继续向上生长．研究表明，60天内，这种瓜苗生长的高度 $y\left(\mathit{cm}\right)$与生长时间 $x$（天 $)$之间的关系大致如图所示．

（1）求 $y$与 $x$之间的函数关系式；

（2）当这种瓜苗长到大约 $80\mathit{cm}$时，开始开花结果，试求这种瓜苗移至大棚后．继续生长大约多少天，开始开花结果？

一辆慢车从甲地匀速行驶至乙地，一辆快车同时从乙地出发匀速行驶至甲地，两车之间的距离 $y$（千米）与行驶时间 $x$（小时）的对应关系如图所示：

（1）甲乙两地相距多远？

（2）求快车和慢车的速度分别是多少？

（3）求出两车相遇后 $y$与 $x$之间的函数关系式；

（4）何时两车相距300千米．

明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积 S（单位： m ²）与工作时间 t（单位： h）之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是（　　）

A．

$300m^2$

B．

$150m^2$

C．

$330m^2$

D．

$450m^2$