初中数学一次函数的应用试题

某市为了鼓励居民节约用水，决定实行两级收费制度．若每月用水量不超过14吨（含14吨），则每吨按政府补贴优惠价 $m$元收费；若每月用水量超过14吨，则超过部分每吨按市场价 $n$元收费．小明家3月份用水20吨，交水费49元；4月份用水18吨，交水费42元．

（1）求每吨水的政府补贴优惠价和市场价分别是多少？

（2）设每月用水量为 $x$吨，应交水费为 $y$元，请写出 $y$与 $x$之间的函数关系式；

（3）小明家5月份用水26吨，则他家应交水费多少元？

小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为 $2500m$，如图是小明和爸爸所走的路程 $s\left(m\right)$与小明步行时间 $t\left(\mathit{min}\right)$的函数图象．

（1）直接写出小明所走路程 $s$与时间 $t$的函数关系式；

（2）小明出发多少时间与爸爸第三次相遇？

（3）在速度都不变的情况下，小明希望比爸爸早 $20\mathit{min}$到达公园，则小明在步行过程中停留的时间需作怎样的调整？

如图，以菱形 $\mathit{ABCD}$对角线交点为坐标原点，建立平面直角坐标系， $A$、 $B$两点的坐标分别为 $(-2\sqrt{5}$， $0)$、 $(0,-\sqrt{5})$，直线 $\mathit{DE}\perp \mathit{DC}$交 $\mathit{AC}$于 $E$，动点 $P$从点 $A$出发，以每秒2个单位的速度沿着 $A\to D\to C$的路线向终点 $C$匀速运动，设 $\mathit{\Delta PDE}$的面积为 $S(S\ne 0)$，点 $P$的运动时间为 $t$秒．

（1）求直线 $\mathit{DE}$的解析式；

（2）求 $S$与 $t$之间的函数关系式，并写出自变量 $t$的取值范围；

（3）当 $t$为何值时， $\angle \mathit{EPD}+\angle \mathit{DCB}=90°$？并求出此时直线 $\mathit{BP}$与直线 $\mathit{AC}$所夹锐角的正切值．

“世界那么大，我想去看看”一句话红遍网络，骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场．顺风车行经营的 $A$型车去年6月份销售总额为3.2万元，今年经过改造升级后 $A$型车每辆销售价比去年增加400元，若今年6月份与去年6月份卖出的 $A$型车数量相同，则今年6月份 $A$型车销售总额将比去年6月份销售总额增加 $25\%$．

（1）求今年6月份 $A$型车每辆销售价多少元（用列方程的方法解答）；

（2）该车行计划7月份新进一批 $A$型车和 $B$型车共50辆，且 $B$型车的进货数量不超过 $A$型车数量的两倍，应如何进货才能使这批车获利最多？

$A$、 $B$两种型号车的进货和销售价格如表：

	$A$型车	$B$型车
进货价格（元 $/$辆）	1100	1400
销售价格（元 $/$辆）	今年的销售价格	2400

某水果基地计划装运甲、乙、丙三种水果到外地销售（每辆汽车规定满载，并且只装一种水果）．如表为装运甲、乙、丙三种水果的重量及利润．

	甲	乙	丙
每辆汽车能装的数量（吨 $)$	4	2	3
每吨水果可获利润（千元）	5	7	4

（1）用8辆汽车装运乙、丙两种水果共22吨到 $A$地销售，问装运乙、丙两种水果的汽车各多少辆？

（2）水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到 $B$地销售（每种水果不少于一车），假设装运甲水果的汽车为 $m$辆，则装运乙、丙两种水果的汽车各多少辆？（结果用 $m$表示）

（3）在（2）问的基础上，如何安排装运可使水果基地获得最大利润？最大利润是多少？

某学校计划组织500人参加社会实践活动，与某公交公司接洽后，得知该公司有 $A$， $B$型两种客车，它们的载客量和租金如表所示：

	$A$型客车	$B$型客车
载客量（人 $/$辆）	45	28
租金（元 $/$辆）	400	250

经测算，租用 $A$， $B$型客车共13辆较为合理，设租用 $A$型客车 $x$辆，根据要求回答下列问题：

（1）用含 $x$的代数式填写下表：

	车辆数（辆 $)$	载客量（人 $)$	租金（元 $)$
$A$型客车	$x$	$45x$	$400x$
$B$型客车	$13-x$

（2）采用怎样的租车方案可以使总的租车费用最低，最低为多少？

为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：

港口	运费（元/吨）
	甲库	乙库
A港	14	20
B港	10	8

（1）设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；

（2）求出最低费用，并说明费用最低时的调配方案．

周末，小芳骑自行车从家出发到野外郊游，从家出发0.5小时到达甲地，游玩一段时间后按原速前往乙地，小芳离家1小时20分钟后，妈妈驾车沿相同路线前往乙地，行驶10分钟时，恰好经过甲地，如图是她们距乙地的路程y（km）与小芳离家时间x（h）的函数图象．

（1）小芳骑车的速度为　　km/h，H点坐标　　．

（2）小芳从家出发多少小时后被妈妈追上？此时距家的路程多远？

（3）相遇后，妈妈载上小芳和自行车同时到达乙地（彼此交流时间忽略不计），求小芳比预计时间早几分钟到达乙地？

甲、乙两车从A城出发前往B城，在整个行程中，两车离开A城的距离y与t的对应关系如图所示：

（1）A、B两城之间距离是多少千米？

（2）求乙车出发多长时间追上甲车？

（3）直接写出甲车出发多长时间，两车相距20千米．

“全民阅读”深入人心，读好书让人终身受益．为打造书香校园，满足同学们的读书需求，学校图书馆准备到新华书店采购文学名著和科技阅读两类图书．经了解，20本文学名著和40本科技阅读共需1520元，一本文学名著比一本科技阅读多22元（注：所采购的文学名著书价格都一样，所采购的科技阅读书价格都一样）．

（1）求每本文学名著和科技阅读各多少元？

（2）若学校要求购买科技阅读比文学名著多20本，科技阅读和文学名著总数不低于72本，总费用不超过2000元，请你为学校求出符合条件的购书方案．

（3）请在（2）的条件下，请你求出此次活动学校最多需投入资金多少元？

甲、乙两车从A城出发前往B城，在整个行程中，两车离开A城的距 离y与时刻t的对应关系，如图所示：

（1）A、B两城之间的距离是多少千米？

（2）求乙车出发后几小时追上甲车？

（3）直接写出甲车出发后多长时间，两车相距20千米．

某绿色食品有限公司准备购进A和B两种蔬菜，B种蔬菜每吨的进价比A中蔬菜每吨的进价多0.5万元，经计算用4.5万元购进的A种蔬菜的吨数与用6万元购进的B种蔬菜的吨数相同，请解答下列问题：

（1）求A，B两种蔬菜每吨的进价；

（2）该公司计划用14万元同时购进A，B两种蔬菜，若A种蔬菜以每吨2万元的价格出售，B种蔬菜以每吨3万元的价格出售，且全部售出，请求出所获利润W（万元）与购买A种蔬菜的资金a（万元）之间的函数关系式；

（3）在（2）的条件下，要求A种蔬菜的吨数不低于B种蔬菜的吨数，若公司欲将（2）中的最大利润全部用于购买甲、乙两种型号的电脑赠给某中学，甲种电脑每台2100元，乙种电脑每台2700元，请直接写出有几种购买电脑的方案．

快、慢两车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早 $\frac{\text{1}}{\text{2}}$小时，慢车速度是快车速度的一半，快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示，请结合图象信息解答下列问题：

（1）请直接写出快、慢两车的速度；

（2）求快车返回过程中y（千米）与x（小时）的函数关系式；

（3）两车出发后经过多长时间相距90千米的路程？直接写出答案．

明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积 S（单位： m ²）与工作时间 t（单位： h）之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是（　　）

A．

$300m^2$

B．

$150m^2$

C．

$330m^2$

D．

$450m^2$

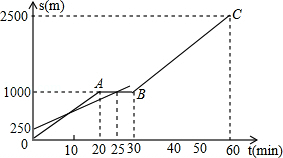
有一科技小组进行了机器人行走性能试验，在试验场地有 A、 B、 C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从 A、 B两点同时同向出发，历时7分钟同时到达 C点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离 y（米）与他们的行走时间 x（分钟）之间的函数图象，请结合图象，回答下列问题：

（1） A、 B两点之间的距离是 　　米，甲机器人前2分钟的速度为 　　米/分；

（2）若前3分钟甲机器人的速度不变，求线段 EF所在直线的函数解析式；

（3）若线段 FG∥ x轴，则此段时间，甲机器人的速度为 　　米/分；

（4）求 A、 C两点之间的距离；

（5）若前3分钟甲机器人的速度不变，直接写出两机器人出发多长时间相距28米．