初中数学一次函数的应用试题

益马高速通车后，将桃江马迹塘的农产品运往益阳的运输成本大大降低，马迹塘一农户需要将 $A$， $B$两种农产品定期运往益阳某加工厂，每次运输 $A$， $B$产品的件数不变，原来每运一次的运费是1200元，现在每运一次的运费比原来减少了300元． $A$， $B$两种产品原来的运费和现在的运费（单位：元 $/$件）如下表所示：

品种	$A$	$B$
原运费	45	25
现运费	30	20

（1）求每次运输的农产品中 $A$， $B$产品各有多少件？

（2）由于该农户诚实守信，产品质量好，加工厂决定提高该农户的供货量，每次运送的产品总件数增加8件，但总件数中 $B$产品的件数不得超过 $A$产品件数的2倍，问产品件数增加后，每次运费最少需要多少元？

某商店销售 $A$型和 $B$型两种电脑，其中 $A$型电脑每台的利润为400元， $B$型电脑每台的利润为500元．该商店计划再一次性购进两种型号的电脑共100台，其中 $B$型电脑的进货量不超过 $A$型电脑的2倍，设购进 $A$型电脑 $x$台，这100台电脑的销售总利润为 $y$元．

（1）求 $y$关于 $x$的函数关系式；

（2）该商店购进 $A$型、 $B$型电脑各多少台，才能使销售总利润最大，最大利润是多少？

（3）实际进货时，厂家对 $A$型电脑出厂价下调 $a(0<a<200)$元，且限定商店最多购进 $A$型电脑60台，若商店保持同种电脑的售价不变，请你根据以上信息，设计出使这100台电脑销售总利润最大的进货方案．

某学校积极响应怀化市“三城同创”的号召，绿化校园，计划购进 $A$， $B$两种树苗，共21棵，已知 $A$种树苗每棵90元， $B$种树苗每棵70元．设购买 $A$种树苗 $x$棵，购买两种树苗所需费用为 $y$元．

（1）求 $y$与 $x$的函数表达式，其中 $0⩽x⩽21$；

（2）若购买 $B$种树苗的数量少于 $A$种树苗的数量，请给出一种费用最省的方案，并求出该方案所需费用．

某水果店5月份购进甲、乙两种水果共花费1700元，其中甲种水果8元 $/$千克，乙种水果18元 $/$千克．6月份，这两种水果的进价上调为：甲种水果10元 $/$千克，乙种水果20元 $/$千克．

（1）若该店6月份购进这两种水果的数量与5月份都相同，将多支付货款300元，求该店5月份购进甲、乙两种水果分别是多少千克？

（2）若6月份将这两种水果进货总量减少到120千克，且甲种水果不超过乙种水果的3倍，则6月份该店需要支付这两种水果的货款最少应是多少元？

自从湖南与欧洲的“湘欧快线”开通后，我省与欧洲各国经贸往来日益频繁，某欧洲客商准备在湖南采购一批特色商品，经调查，用16000元采购 $A$型商品的件数是用7500元采购 $B$型商品的件数的2倍，一件 $A$型商品的进价比一件 $B$型商品的进价多10元．

（1）求一件 $A$， $B$型商品的进价分别为多少元？

（2）若该欧洲客商购进 $A$， $B$型商品共250件进行试销，其中 $A$型商品的件数不大于 $B$型的件数，且不小于80件．已知 $A$型商品的售价为240元 $/$件， $B$型商品的售价为220元 $/$件，且全部售出．设购进 $A$型商品 $m$件，求该客商销售这批商品的利润 $v$与 $m$之间的函数关系式，并写出 $m$的取值范围；

（3）在（2）的条件下，欧洲客商决定在试销活动中每售出一件 $A$型商品，就从一件 $A$型商品的利润中捐献慈善资金 $a$元，求该客商售完所有商品并捐献慈善资金后获得的最大收益．

永州市是一个降水丰富的地区，今年4月初，某地连续降雨导致该地某水库水位持续上涨，下表是该水库4月1日 $~4$月4日的水位变化情况：

日期 $x$	1	2	3	4
水位 $y$（米 $)$	20.00	20.50	21.00	21.50

（1）请建立该水库水位 $y$与日期之间的函数模型；

（2）请用求出的函数表达式预测该水库今年4月6日的水位；

（3）你能用求出的函数表达式预测该水库今年12月1日的水位吗？

为响应绿色出行号召，越来越多市民选择租用共享单车出行，已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式，如图描述了两种方式应支付金额 $y$（元 $)$与骑行时间 $x$（时 $)$之间的函数关系，根据图象回答下列问题：

（1）求手机支付金额 $y$（元 $)$与骑行时间 $x$（时 $)$的函数关系式；

（2）李老师经常骑行共享单车，请根据不同的骑行时间帮他确定选择哪种支付方式比较合算．

某工厂有甲种原料 $130\mathit{kg}$，乙种原料 $144\mathit{kg}$．现用这两种原料生产出 $A$， $B$两种产品共30件．已知生产每件 $A$产品需甲种原料 $5\mathit{kg}$，乙种原料 $4\mathit{kg}$，且每件 $A$产品可获利700元；生产每件 $B$产品需甲种原料 $3\mathit{kg}$，乙种原料 $6\mathit{kg}$，且每件 $B$产品可获利900元．设生产 $A$产品 $x$件（产品件数为整数件），根据以上信息解答下列问题：

（1）生产 $A$， $B$两种产品的方案有哪几种；

（2）设生产这30件产品可获利 $y$元，写出 $y$关于 $x$的函数解析式，写出（1）中利润最大的方案，并求出最大利润．

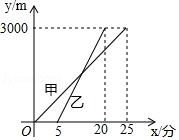
“低碳环保，绿色出行”的理念得到广大群众的接受，越来越多的人喜欢选择自行车作为出行工具．小军和爸爸同时从家骑自行车去图书馆，爸爸先以150米 $/$分的速度骑行一段时间，休息了5分钟，再以 $m$米 $/$分的速度到达图书馆，小军始终以同一速度骑行，两人行驶的路程 $y$（米 $)$与时间 $x$（分钟）的关系如图，请结合图象，解答下列问题：

（1） $a=$　　， $b=$　　， $m=$　　；

（2）若小军的速度是120米 $/$分，求小军在途中与爸爸第二次相遇时，距图书馆的距离；

（3）在（2）的条件下，爸爸自第二次出发至到达图书馆前，何时与小军相距100米？

（4）若小军的行驶速度是 $v$米 $/$分，且在途中与爸爸恰好相遇两次（不包括家、图书馆两地），请直接写出 $v$的取值范围．

在水果销售旺季，某水果店购进一优质水果，进价为20元 $/$千克，售价不低于20元 $/$千克，且不超过32元 $/$千克，根据销售情况，发现该水果一天的销售量 $y$（千克）与该天的售价 $x$（元 $/$千克）满足如下表所示的一次函数关系．

销售量 $y$（千克）	$\dots$	34.8	32	29.6	28	$\dots$
售价 $x$（元 $/$千克）	$\dots$	22.6	24	25.2	26	$\dots$

（1）某天这种水果的售价为23.5元 $/$千克，求当天该水果的销售量．

（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？

学校准备购进一批甲、乙两种办公桌若干张，并且每买1张办公桌必须买2把椅子，椅子每把100元，若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元；购买10张甲种办公桌比购买5张乙种办公桌多花费2000元．

（1）求甲、乙两种办公桌每张各多少元？

（2）若学校购买甲乙两种办公桌共40张，且甲种办公桌数量不多于乙种办公桌数量的3倍，请你给出一种费用最少的方案，并求出该方案所需费用．

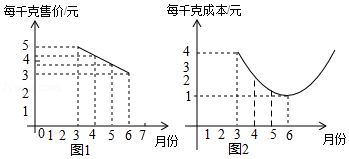
某种蔬菜的销售单价 $y_1$与销售月份 $x$之间的关系如图1所示，成本 $y_2$与销售月份 $x$之间的关系如图2所示（图1的图象是线段，图2的图象是抛物线）

（1）已知6月份这种蔬菜的成本最低，此时出售每千克的收益是多少元？（收益 $=$售价 $-$成本）

（2）哪个月出售这种蔬菜，每千克的收益最大？简单说明理由．

（3）已知市场部销售该种蔬菜4、5两个月的总收益为22万元，且5月份的销售量比4月份的销售量多2万千克，求4、5两个月的销售量分别是多少万千克？

赛龙舟是端午节的主要习俗，某市甲乙两支龙舟队在端午节期间进行划龙舟比赛，从起点 $A$驶向终点 $B$，在整个行程中，龙舟离开起点的距离 $y$（米 $)$与时间 $x$（分钟）的对应关系如图所示，请结合图象解答下列问题：

（1）起点 $A$与终点 $B$之间相距多远？

（2）哪支龙舟队先出发？哪支龙舟队先到达终点？

（3）分别求甲、乙两支龙舟队的 $y$与 $x$函数关系式；

（4）甲龙舟队出发多长时间时两支龙舟队相距200米？

某商店以20元 $/$千克的单价新进一批商品，经调查发现，在一段时间内，销售量 $y$（千克）与销售单价 $x$（元 $/$千克）之间为一次函数关系，如图所示．

（1）求 $y$与 $x$的函数表达式；

（2）要使销售利润达到800元，销售单价应定为每千克多少元？

某校为了在九月份迎接高一年级的新生，决定将学生公寓楼重新装修．现学校招用了甲、乙两个工程队．若两队合作，8天就可以完成该项工程；若由甲队先单独做3天后，剩余部分由乙队单独做需要18天才能完成．

（1）求甲、乙两队工作效率分别是多少？

（2）甲队每天工资3000元，乙队每天工资1400元．学校要求在12天内将学生公寓楼装修完成．若完成该工程甲队工作 $m$天，乙队工作 $n$天．求学校需支付的总工资 $w$（元 $)$与甲队工作天数 $m$（天 $)$的函数关系式，并求出 $m$的取值范围及 $w$的最小值．