初中数学一次函数的应用试题

某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出．据市场调查，若按每个玩具280元销售时，每月可销售300个．若销售单价每降低1元，每月可多售出2个．据统计，每个玩具的固定成本 $Q$（元）与月产销量 $y$（个）满足如下关系：

月产销量 $y$（个）	$\dots$	160	200	240	300	$\dots$
每个玩具的固定成本 $Q$（元）	$\dots$	60	48	40	32	$\dots$

（1）写出月产销量 $y$（个）与销售单价 $x$（元）之间的函数关系式；

（2）求每个玩具的固定成本 $Q$（元）与月产销量 $y$（个）之间的函数关系式；

（3）若每个玩具的固定成本为30元，则它占销售单价的几分之几？

（4）若该厂这种玩具的月产销量不超过400个，则每个玩具的固定成本至少为多少元？销售单价最低为多少元？

现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品 $x$千克．

（1）请分别写出甲、乙两家快递公司快递该物品的费用 $y$（元）与 $x$（千克）之间的函数关系式；

（2）小明选择哪家快递公司更省钱？

星期天，李玉刚同学随爸爸妈妈回老家探望爷爷奶奶，爸爸 $\mathit{8}\mathit{:}\mathit{30}$骑自行车先走，平均每小时骑行 $\mathit{20}\mathit{km}$；李玉刚同学和妈妈 $\mathit{9}\mathit{:}\mathit{30}$乘公交车后行，公交车平均速度是 $\mathit{40}\mathit{km}\mathit{/}\mathit{h}$．爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同，路程均为 $\mathit{40}\mathit{km}$．设爸爸骑行时间为 $\mathit{x}\mathit{\left(}\mathit{h}\mathit{\right)}$．

（1）请分别写出爸爸的骑行路程 ${\mathit{y}}_{\mathit{1}}\mathit{\left(}\mathit{km}\mathit{\right)}$、李玉刚同学和妈妈的乘车路程 ${\mathit{y}}_{\mathit{2}}\mathit{\left(}\mathit{k}\mathit{m}\mathit{\right)}$与 $\mathit{x}\mathit{\left(}\mathit{h}\mathit{\right)}$之间的函数解析式，并注明自变量的取值范围；

（2）请在同一个平面直角坐标系中画出（1）中两个函数的图象；

（3）请回答谁先到达老家．

今年是“精准扶贫”攻坚关键年，某扶贫工作队为对口扶贫村引进建立了一村集体企业，并无偿提供一笔无息贷款作为启动资金，双方约定：①企业生产出的产品全部由扶贫工作队及时联系商家收购；②企业从生产销售的利润中，要保证按时发放工人每月最低工资32000元．已知该企业生产的产品成本为20元 $/$件，月生产量 $y$（千件）与出厂价 $x$（元 $\left)\right(25⩽x⩽50)$的函数关系可用图中的线段 $\mathit{AB}$和 $\mathit{BC}$表示，其中 $\mathit{AB}$的解析式为 $y=-\frac{1}{20}x+m(m$为常数）．

（1）求该企业月生产量 $y$（千件）与出厂价 $x$（元 $)$之间的函数关系式，并写出自变量 $x$的取值范围．

（2）当该企业生产出的产品出厂价定为多少元时，月利润 $W$（元 $)$最大？最大利润是多少？ $[$月利润 $=$（出厂价 $-$成本） $\times$月生产量 $-$工人月最低工资 $]$．

如图，已知菱形 $\mathit{OABC}$的边 $\mathit{OA}$在 $x$轴上，点 $B$的坐标为 $(8,4)$，点 $P$是对角线 $\mathit{OB}$上的一个动点，点 $D(0,2)$在 $y$轴上，当 $\mathit{CP}+\mathit{DP}$最短时，点 $P$的坐标为　　．

某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，日销售量 $y\left(\mathit{kg}\right)$与时间第 $t$天之间的函数关系式为 $y=2t+100(1⩽t⩽80$， $t$为整数），销售单价 $p$（元 $/\mathit{kg})$与时间第 $t$天之间满足一次函数关系如下表：

时间第 $t$天	1	2	3	$\dots$	80
销售单价 $p/$（元 $/\mathit{kg})$	49.5	49	48.5	$\dots$	10

（1）直接写出销售单价 $p$（元 $/\mathit{kg})$与时间第 $t$天之间的函数关系式．

（2）在整个销售旺季的80天里，哪一天的日销售利润最大？最大利润是多少？

在综合与实践活动中，活动小组对学校400米的跑道进行规划设计，跑道由两段直道和两端是半圆弧的跑道组成．其中400米跑道最内圈为400米，两端半圆弧的半径为36米． $(\pi$ 取 $3.14)$ ．

（1）求400米跑道中一段直道的长度；

（2）在活动中发现跑道周长（单位：米）随跑道宽度（距最内圈的距离，单位：米）的变化而变化．请完成下表：

跑道宽度 $/$ 米	0	1	2	3	4	5	$\dots$
跑道周长 $/$ 米	400						$\dots$

若设 $x$ 表示跑道宽度（单位：米）， $y$ 表示该跑道周长（单位：米），试写出 $y$ 与 $x$ 的函数关系式：

（3）将446米的跑道周长作为400米跑道场地的最外沿，那么它与最内圈（跑道周长400米）形成的区域最多能铺设道宽为1.2米的跑道多少条？

将直角三角板 $\mathit{ABC}$ 按如图1放置，直角顶点 $C$ 与坐标原点重合，直角边 $\mathit{AC}$ 、 $\mathit{BC}$ 分别与 $x$ 轴和 $y$ 轴重合，其中 $\angle \mathit{ABC}=30°$ ．将此三角板沿 $y$ 轴向下平移，当点 $B$ 平移到原点 $O$ 时运动停止．设平移的距离为 $m$ ，平移过程中三角板落在第一象限部分的面积为 $s$ ， $s$ 关于 $m$ 的函数图象（如图2所示）与 $m$ 轴相交于点 $P(\sqrt{3}$ ， $0)$ ，与 $s$ 轴相交于点 $Q$ ．

（1）试确定三角板 $\mathit{ABC}$ 的面积；

（2）求平移前 $\mathit{AB}$ 边所在直线的解析式；

（3）求 $s$ 关于 $m$ 的函数关系式，并写出 $Q$ 点的坐标．

为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水，对居民家庭每户每月用水量采用分档递增收费的方式，每户每月用水量不超过基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费．为对基本用水量进行决策，随机抽查2000户居民家庭每户每月用水量的数据，整理绘制出下面的统计表：

用户每月用水量 $\left(m^3\right)$	32及其以下	33	34	35	36	37	38	39	40	41	42	43及其以上
户数（户）	200	160	180	220	240	210	190	100	170	120	100	110

（1）为确保 $70\%$ 的居民家庭每户每月的基本用水量需求，那么每户每月的基本用水量最低应确定为多少立方米？

（2）若将（1）中确定的基本用水量及其以内的部分按每立方米1.8元交费，超过基本用水量的部分按每立方米2.5元交费．设 $x$ 表示每户每月用水量（单位： $m^3$ ）， $y$ 表示每户每月应交水费（单位：元），求 $y$ 与 $x$ 的函数关系式；

（3）某户家庭每月交水费是80.9元，请按以上收费方式计算该家庭当月用水量是多少立方米？

某商店分两次购进 $A$ 、 $B$ 两种商品进行销售，两次购进同一种商品的进价相同，具体情况如下表所示：

	购进数量（件）		购进所需费用（元）
	$A$	$B$
第一次	30	40	3800
第二次	40	30	3200

（1）求 $A$ 、 $B$ 两种商品每件的进价分别是多少元？

（2）商场决定 $A$ 种商品以每件30元出售， $B$ 种商品以每件100元出售．为满足市场需求，需购进 $A$ 、 $B$ 两种商品共1000件，且 $A$ 种商品的数量不少于 $B$ 种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

某种水彩笔，在购买时，若同时额外购买笔芯，每个优惠价为3元，使用期间，若备用笔芯不足时需另外购买，每个5元．现要对在购买水彩笔时应同时购买几个笔芯作出选择，为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据，整理绘制出下面的条形统计图：

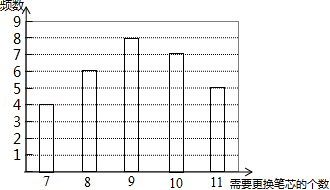
设 $x$ 表示水彩笔在使用期内需要更换的笔芯个数， $y$ 表示每支水彩笔在购买笔芯上所需要的费用（单位：元）， $n$ 表示购买水彩笔的同时购买的笔芯个数．

（1）若 $n=9$ ，求 $y$ 与 $x$ 的函数关系式；

（2）若要使这30支水彩笔"更换笔芯的个数不大于同时购买笔芯的个数"的频率不小于0.5，确定 $n$ 的最小值；

（3）假设这30支笔在购买时，每支笔同时购买9个笔芯，或每支笔同时购买10个笔芯，分别计算这30支笔在购买笔芯所需费用的平均数，以费用最省作为选择依据，判断购买一支水彩笔的同时应购买9个还是10个笔芯．

小强与小刚都住在安康小区，在同一所学校读书，某天早上，小强 $7:30$从安康小区站乘坐校车去学校，途中需停靠两个站点才能到达学校站点，且每个站点停留2分钟，校车行驶途中始终保持匀速，当天早上，小刚 $7:39$从安康小区站乘坐出租车沿相同路线出发，出租车匀速行驶，比小强乘坐的校车早1分钟到学校站点，他们乘坐的车辆从安康小区站出发所行使路程 $y$（千米）与校车行驶时间 $x$（分钟）之间的函数图象如图所示．

（1）求点 $A$的纵坐标 $m$的值；

（2）小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车？并求此时他们距学校站点的路程．

某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需付的行李费 $y$（元）是行李质量 $x\left(\mathit{kg}\right)$的一次函数．已知行李质量为 $20\mathit{kg}$时需付行李费2元，行李质量为 $50\mathit{kg}$时需付行李费8元．

（1）当行李的质量 $x$超过规定时，求 $y$与 $x$之间的函数表达式；

（2）求旅客最多可免费携带行李的质量．

张老师计划到超市购买甲种文具100个，他到超市后发现还有乙种文具可供选择．如果调整文具的购买品种，每减少购买1个甲种文具，需增加购买2个乙种文具．设购买 $x$个甲种文具时，需购买 $y$个乙种文具．

（1）①当减少购买1个甲种文具时， $x=$　    　， $y=$　   　；

②求 $y$与 $x$之间的函数表达式．

（2）已知甲种文具每个5元，乙种文具每个3元，张老师购买这两种文具共用去540元．甲、乙两种文具各购买了多少个？

某蓝莓种植生产基地产销两旺，采摘的蓝莓部分加工销售，部分直接销售，且当天都能销售完，直接销售是40元 $/$斤，加工销售是130元 $/$斤（不计损耗）．已知基地雇佣20名工人，每名工人只能参与采摘和加工中的一项工作，每人每天可以采摘70斤或加工35斤．设安排 $x$名工人采摘蓝莓，剩下的工人加工蓝莓．

（1）若基地一天的总销售收入为 $y$元，求 $y$与 $x$的函数关系式；

（2）试求如何分配工人，才能使一天的销售收入最大？并求出最大值．