小明从家步行到学校需走的路程为1800米.图中的折线 反映了小明从家步行到学校所走的路程 (米 与时间 (分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.

某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约 时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度 与生长时间 (天 之间的关系大致如图所示.
(1)求 与 之间的函数关系式;
(2)当这种瓜苗长到大约 时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?

学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离 (米 与时间 (分钟)之间的函数关系如图所示.
(1)根据图象信息,当 分钟时甲乙两人相遇,甲的速度为 米 分钟;
(2)求出线段 所表示的函数表达式.

一水果店是 酒店某种水果的首选供货商,水果店根据该酒店以往每月的需求情况,本月初专门为他们准备了 的这种水果.已知水果店每售出 该水果可获利润10元,未售出的部分每 将亏损6元,以 (单位: , 表示 酒店本月对这种水果的需求量, (元 表示水果店销售这批水果所获得的利润.
(1)求 关于 的函数表达式;
(2)问:当 酒店本月对这种水果的需求量如何时,该水果店销售这批水果所获的利润不少于22000元?
蚊香长度 (厘米)与燃烧时间 (小时)之间的函数表达式为 .则蚊香燃烧的速度是
A.10厘米 小时B.105厘米 小时
C.10.5厘米 小时D.不能确定
某种型号汽车油箱容量为 ,每行驶 耗油 .设一辆加满油的该型号汽车行驶路程为 ,行驶过程中油箱内剩余油量为 .
(1)求 与 之间的函数表达式;
(2)为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的 ,按此建议,求该辆汽车最多行驶的路程.
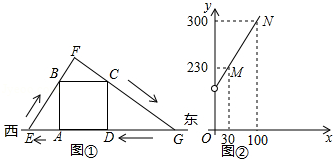
如图①,直线 表示一条东西走向的笔直公路,四边形 是一块边长为100米的正方形草地,点 , 在直线 上,小明从点 出发,沿公路 向西走了若干米后到达点 处,然后转身沿射线 方向走到点 处,接着又改变方向沿射线 方向走到公路 上的点 处,最后沿公路 回到点 处.设 米(其中 , 米,已知 与 之间的函数关系如图②所示,
(1)求图②中线段 所在直线的函数表达式;
(2)试问小明从起点 出发直至最后回到点 处,所走过的路径(即 是否可以是一个等腰三角形?如果可以,求出相应 的值;如果不可以,说明理由.
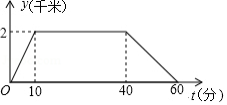
小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第 回到家中.设小明出发第 时的速度为 ,离家的距离为 , 与 之间的函数关系如图所示(图中的空心圈表示不包含这一点).
(1)小明出发第 时离家的距离为 ;
(2)当 时,求 与 之间的函数表达式;
(3)画出 与 之间的函数图象.

某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调查.获取信息如下:
购买数量低于5000块 |
购买数量不低于5000块 |
|
红色地砖 |
原价销售 |
以八折销售 |
蓝色地砖 |
原价销售 |
以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
如图,公交车行驶在笔直的公路上,这条路上有 , , , 四个站点,每相邻两站之间的距离为5千米,从 站开往 站的车称为上行车,从 站开往 站的车称为下行车,第一班上行车、下行车分别从 站、 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 , 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米 小时.

(1)问第一班上行车到 站、第一班下行车到 站分别用时多少?
(2)若第一班上行车行驶时间为 小时,第一班上行车与第一班下行车之间的距离为 千米,求 与 的函数关系式;
(3)一乘客前往 站办事,他在 , 两站间的 处(不含 , 站),刚好遇到上行车, 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到 站或走到 站乘下行车前往 站.若乘客的步行速度是5千米 小时,求 满足的条件.
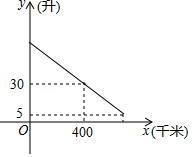
一辆汽车行驶时的耗油量为0.1升 千米,如图是油箱剩余油量 (升 关于加满油后已行驶的路程 (千米)的函数图象.
(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
星期天,小明上午 从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离 (千米)与时间 (分钟)的关系如图所示,则上午 小明离家的距离是 千米.
某通讯公司就上宽带网推出 , , 三种月收费方式.这三种收费方式每月所需的费用 (元 与上网时间 的函数关系如图所示,则下列判断错误的是

A.每月上网时间不足 时,选择 方式最省钱
B.每月上网费用为60元时, 方式可上网的时间比 方式多
C.每月上网时间为 时,选择 方式最省钱
D.每月上网时间超过 时,选择 方式最省钱
“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向 , 两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥; , 两个果园分别需用110吨和70吨有机化肥.两个仓库到 , 两个果园的路程如表所示:
路程(千米) |
||
甲仓库 |
乙仓库 |
|
果园 |
15 |
25 |
果园 |
20 |
20 |
设甲仓库运往 果园 吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.
运量(吨 |
运费(元 |
|||
甲仓库 |
乙仓库 |
甲仓库 |
乙仓库 |
|
果园 |
|
|
|
|
果园 |
|
|
|
|
(2)设总运费为 元,求 关于 的函数表达式,并求当甲仓库运往 果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
试题篮
()