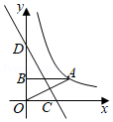
如图,反比例函数 的图象经过点 ,过 作 轴于点 ,连 ,直线 ,交 轴于点 ,交 轴于点 ,若点 关于直线 的对称点 恰好落在该反比例函数图像上,则 点纵坐标为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知反比例函数 的图象经过点 , 轴,且 的面积为2.
(1)求 和 的值;
(2)若点 也在反比例函数 的图象上,当 时,求函数值 的取值范围.

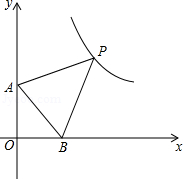
如图,已知 A( , y 1), B(2, y 2)为反比例函数 y= 图象上的两点,动点 P( x,0)在 x轴的正半轴上运动,当线段 AP与线段 BP之差达到最大时点 P的坐标是( )

| A. |
( ,0) |
B. |
(3,0) |
C. |
(4,0) |
D. |
( ,0) |
以矩形 ABCD两条对角线的交点 O为坐标原点,以平行于两边的方向为坐标轴,建立如图所示的平面直角坐标系, BE⊥ AC,垂足为 E.若双曲线 y=( x>0)经过点 D,则 OB• BE的值为 .

如图,在平面直角坐标系 中,函数 的图象经过菱形 的顶点 和边 的中点 ,若菱形 的边长为3,则 的值为 .

如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ,1)在反比例函数 的图象上.
(1)求反比例函数 的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.

已知反比例函数 y= ( k为常数).
(1)若点 P 1( , y 1)和点 P 2(﹣ , y 2)是该反比例函数图象上的两点,试利用反比例函数的性质比较 y 1和 y 2的大小;
(2)设点 P( m, n)( m>0)是其图象上的一点,过点 P作 PM⊥ x轴于点 M.若tan∠ POM=2, PO= ( O为坐标原点),求 k的值,并直接写出不等式 kx+ >0的解集.
将一副三角板如图放置在平面直角坐标系中,顶点 与原点 重合, 在 轴正半轴上,且 ,点 在 上, ,将这副三角板整体向右平移 个单位, , 两点同时落在反比例函数 的图象上.

如图,在直角坐标系中,以坐标原点 , , 为顶点的 ,其两个锐角对应的外角角平分线相交于点 ,且点 恰好在反比例函数 的图象上,则 的值为
A.36B.48C.49D.64
如图,点 , 在反比例函数 的图象上, 轴, 轴,垂足 , 分别在 轴的正、负半轴上, ,已知 , 是 的中点,且 的面积是 的面积的2倍,则 的值是 .
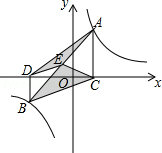
如图, 的三个顶点分别为 , , .若反比例函数 在第一象限内的图象与 有交点,则 的取值范围是

| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()