如图,四边形 的四个顶点分别在反比例函数 与 的图象上,对角线 轴,且 于点 .已知点 的横坐标为4.
(1)当 , 时.
①若点 的纵坐标为2,求直线 的函数表达式.
②若点 是 的中点,试判断四边形 的形状,并说明理由.
(2)四边形 能否成为正方形?若能,求此时 , 之间的数量关系;若不能,试说明理由.

如图,一次函数 的图象与反比例函数 的图象在第二象限交于点 ,过点 作 轴于点 ,一次函数的图象分别交 、 轴于点 、 , ,
(1)求点 的坐标;
(2)求一次函数与反比例函数的表达式;
(3)根据图象直接写出不等式 的解集.

如图,在平面直角坐标系中,将坐标原点 沿 轴向左平移2个单位长度得到点 ,过点 作 轴的平行线交反比例函数 的图象于点 , .
(1)求反比例函数的解析式;
(2)若 , 、 , 是该反比例函数图象上的两点,且 时, ,指出点 、 各位于哪个象限?并简要说明理由.

如图,在矩形 中, , , 是 上的一个动点 不与 , 重合),过点 的反比例函数 的图象与 边交于点 .
(1)当 为 的中点时,求该函数的解析式;
(2)当 为何值时, 的面积最大,最大面积是多少?

如图,在平面直角坐标系中,矩形 的顶点 的坐标为 ,直线 与边 , 分别相交于点 , ,函数 的图象过点 .
(1)试说明点 也在函数 的图象上;
(2)将直线 沿 轴的负方向平移得到直线 ,当直线 与函数 的图象仅有一个交点时,求直线 的解析式.

如图, , 是反比例函数 图象上的两点,过点 作 轴,垂足为 , 交 于点 .若 为 的中点, 的面积为3,则 的值为 .
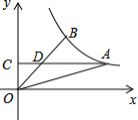
如图,在平面直角坐标系 中,双曲线 经过 的顶点 , .点 的坐标为 ,点 在 轴上,且 轴, .
(1)填空:点 的坐标为 ;
(2)求双曲线和 所在直线的解析式.

在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标为 ,顶点 恰好落在第一象限的双曲线上,现将直角三角板沿 轴正方向平移,当顶点 恰好落在该双曲线上时停止运动,则此时点 的对应点 的坐标为

A. , B. C. , D.
如图, ,直角边分别落在 轴和 轴上,斜边相交于点 ,且 .若四边形 的面积为6,反比例函数 的图象经过点 ,则 的值为 .

如图, 的顶点 在坐标原点,点 在 轴上, , , ,反比例函数 的图象经过 的中点 ,交 于点 .
(1)求反比例函数的关系式;
(2)连接 ,求四边形 的面积.

如图,一次函数 的图象与反比例函数 的图象交于点 、 ,与 轴交于点 ,若 ,且 .
(1)求反比例函数与一次函数的表达式;
(2)请直接写出不等式 的解集.
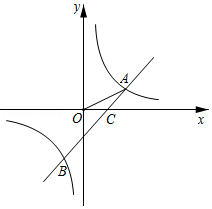
如图,直线 与反比例函数 的图象相交于 和 两点
(1)求 的值;
(2)直线 与直线 相交于点 ,与反比例函数的图象相交于点 .若 ,求 的值;
(3)直接写出不等式 的解集.

如图1,一次函数 与反比例函数 的图象交于点 , ,与 轴交于点 ,直线 与反比例函数 的图象的另一支交于点 ,过点 作直线 垂直于 轴,点 是点 关于直线 的对称点.
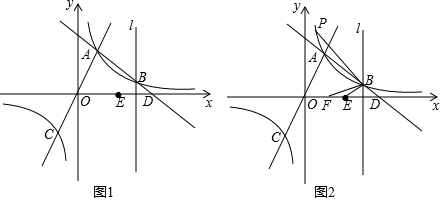
(1) ;
(2)判断点 、 、 是否在同一条直线上,并说明理由;
(3)如图2,已知点 在 轴正半轴上, ,点 是反比例函数 的图象位于第一象限部分上的点(点 在点 的上方), ,则点 的坐标为 , .
试题篮
()