初中数学反比例函数与一次函数的交点问题解答题

如图，已知点 $D$在反比例函数 $y=\frac{a}{x}$的图象上，过点 $D$作 $\mathit{DB}\perp y$轴，垂足为 $B(0,3)$，直线 $y=\mathit{kx}+b$经过点 $A(5,0)$，与 $y$轴交于点 $C$，且 $\mathit{BD}=\mathit{OC}$， $\mathit{OC}:\mathit{OA}=2:5$．

（1）求反比例函数 $y=\frac{a}{x}$和一次函数 $y=\mathit{kx}+b$的表达式；

（2）直接写出关于 $x$的不等式 $\frac{a}{x}>\mathit{kx}+b$的解集．

如图，在平面直角坐标系中，点 $O$为坐标原点，菱形 $\mathit{OABC}$的顶点 $A$在 $x$轴的正半轴上，顶点 $C$的坐标为 $(1,\sqrt{3})$．

（1）求图象过点 $B$的反比例函数的解析式；

（2）求图象过点 $A$， $B$的一次函数的解析式；

（3）在第一象限内，当以上所求一次函数的图象在所求反比例函数的图象下方时，请直接写出自变量 $x$的取值范围．

如图，一次函数 $y=\mathit{kx}+b$与反比例函数 $y=\frac{a}{x}$的图象在第一象限交于 $A$、 $B$两点， $B$点的坐标为 $(3,2)$，连接 $\mathit{OA}$、 $\mathit{OB}$，过 $B$作 $\mathit{BD}\perp y$轴，垂足为 $D$，交 $\mathit{OA}$于 $C$，若 $\mathit{OC}=\mathit{CA}$．

（1）求一次函数和反比例函数的表达式；

（2）求 $\mathit{\Delta AOB}$的面积．

如图，一次函数 $y=\mathit{kx}+b$的图象与坐标轴分别交于 $A$、 $B$两点，与反比例函数 $y=\frac{n}{x}$的图象在第一象限的交点为 $C$， $\mathit{CD}\perp x$轴，垂足为 $D$，若 $\mathit{OB}=3$， $\mathit{OD}=6$， $\mathit{\Delta AOB}$的面积为3．

（1）求一次函数与反比例函数的解析式；

（2）直接写出当 $x>0$时， $\mathit{kx}+b-\frac{n}{x}<0$的解集．

有这样一个问题：探究同一平面直角坐标系中系数互为倒数的正、反比例函数 $y=\frac{1}{k}x$与 $y=\frac{k}{x}(k\ne 0)$的图象性质．

小明根据学习函数的经验，对函数 $y=\frac{1}{k}x$与 $y=\frac{k}{x}$，当 $k>0$时的图象性质进行了探究．

下面是小明的探究过程：

（1）如图所示，设函数 $y=\frac{1}{k}x$与 $y=\frac{k}{x}$图象的交点为 $A$， $B$，已知 $A$点的坐标为 $(-k,-1)$，则 $B$点的坐标为　　；

（2）若点 $P$为第一象限内双曲线上不同于点 $B$的任意一点．

①设直线 $\mathit{PA}$交 $x$轴于点 $M$，直线 $\mathit{PB}$交 $x$轴于点 $N$．求证： $\mathit{PM}=\mathit{PN}$．

证明过程如下：设 $P(m,\frac{k}{m})$，直线 $\mathit{PA}$的解析式为 $y=\mathit{ax}+b(a\ne 0)$．

则 $\left\{\begin{array}{c}-\mathit{ka}+b=-1\\ \mathit{ma}+b=\frac{k}{m}\end{array}\right.$，

解得 $\left\{\begin{array}{c}a=\\ b=\end{array}\right.$　　

$\therefore$直线 $\mathit{PA}$的解析式为　　

请你把上面的解答过程补充完整，并完成剩余的证明．

②当 $P$点坐标为 $(1$， $k\left)\right(k\ne 1)$时，判断 $\mathit{\Delta PAB}$的形状，并用 $k$表示出 $\mathit{\Delta PAB}$的面积．

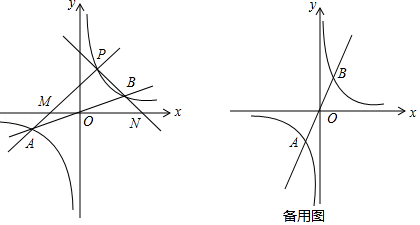
如图，一次函数 $y=\mathit{kx}+2$的图象与反比例函数 $y=\frac{m}{x}(x<0)$的图象在第二象限交于点 $P$，过点 $P$作 $\mathit{PA}\perp x$轴于点 $A$，一次函数的图象分别交 $x$、 $y$轴于点 $C$、 $B$， $S_{\mathit{\Delta OBC}}=1$， $\mathit{OA}=\mathit{OC}$

（1）求点 $B$的坐标；

（2）求一次函数与反比例函数的表达式；

（3）根据图象直接写出不等式 $\mathit{kx}+2>\frac{m}{x}$的解集．

如图，直线 $y=3x$与双曲线 $y=\frac{k}{x}(k\ne 0,x>0)$交于点 $A$，点 $A$的横坐标是1．

（1）求点 $A$的坐标及双曲线的解析式；

（2）点 $B$是双曲线上一点，且点 $B$的纵坐标是1，连接 $\mathit{OB}$， $\mathit{AB}$，求 $\mathit{\Delta AOB}$的面积．

如图1，一次函数 $y=\mathit{kx}-3(k\ne 0)$的图象与 $y$轴交于点 $A$，与反比例函数 $y=\frac{4}{x}(x>0)$的图象交于点 $B(4,b)$．

（1） $b=$　     　； $k=$　    　；

（2）点 $C$是线段 $\mathit{AB}$上的动点（与点 $A$、 $B$不重合），过点 $C$且平行于 $y$轴的直线 $l$交这个反比例函数的图象于点 $D$，求 $\mathit{\Delta OCD}$面积的最大值；

（3）将（2）中面积取得最大值的 $\mathit{\Delta OCD}$沿射线 $\mathit{AB}$方向平移一定的距离，得到△ $O\text{'}C\text{'}D\text{'}$，若点 $O$的对应点 $O\text{'}$落在该反比例函数图象上（如图 $2)$，则点 $D\text{'}$的坐标是　 　．

如图，一次函数 $y=k_{1}x+b$的图象与 $x$轴、 $y$轴分别交于 $A$， $B$两点，与反比例函数 $y=\frac{k_2}{x}$的图象分别交于 $C$， $D$两点，点 $C(2,4)$，点 $B$是线段 $\mathit{AC}$的中点．

（1）求一次函数 $y=k_{1}x+b$与反比例函数 $y=\frac{k_2}{x}$的解析式；

（2）求 $\mathit{\Delta COD}$的面积；

（3）直接写出当 $x$取什么值时， $k_{1}x+b<\frac{k_2}{x}$．

如图，在平面直角坐标系 $\mathit{xOy}$中，点 $A(3,2)$在反比例函数 $y=\frac{k}{x}(x>0)$的图象上，点 $B$在 $\mathit{OA}$的延长线上， $\mathit{BC}\perp x$轴，垂足为 $C$， $\mathit{BC}$与反比例函数的图象相交于点 $D$，连接 $\mathit{AC}$， $\mathit{AD}$．

（1）求该反比例函数的解析式；

（2）若 $S_{\mathit{\Delta ACD}}=\frac{3}{2}$，设点 $C$的坐标为 $(a,0)$，求线段 $\mathit{BD}$的长．

如图，在平面直角坐标系中，一次函数 $y=\mathit{mx}+n(m\ne 0)$的图象与 $y$轴交于点 $C$，与反比例函数 $y=\frac{k}{x}(k\ne 0)$的图象交于 $A$， $B$两点，点 $A$在第一象限，纵坐标为4，点 $B$在第三象限， $\mathit{BM}\perp x$轴，垂足为点 $M$， $\mathit{BM}=\mathit{OM}=2$．

（1）求反比例函数和一次函数的解析式．

（2）连接 $\mathit{OB}$， $\mathit{MC}$，求四边形 $\mathit{MBOC}$的面积．

如图，在平面直角坐标系中，一次函数 $y=\mathit{mx}+n(m\ne 0)$的图象与 $y$轴交于点 $C$，与反比例函数 $y=\frac{k}{x}(k\ne 0)$的图象交于 $A$， $B$两点，点 $A$在第一象限，纵坐标为4，点 $B$在第三象限， $\mathit{BM}\perp x$轴，垂足为点 $M$， $\mathit{BM}=\mathit{OM}=2$．

（1）求反比例函数和一次函数的解析式．

（2）连接 $\mathit{OB}$， $\mathit{MC}$，求四边形 $\mathit{MBOC}$的面积．

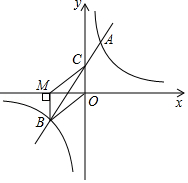
如图，一次函数 $y=\mathit{kx}+b(k\ne 0)$的图象与反比例函数 $y=\frac{a}{x}(a\ne 0)$的图象在第二象限交于点 $A(m,2)$．与 $x$轴交于点 $C(-1,0)$．过点 $A$作 $\mathit{AB}\perp x$轴于点 $B$， $\mathit{\Delta ABC}$的面积是3．

（1）求一次函数和反比例函数的解析式；

（2）若直线 $\mathit{AC}$与 $y$轴交于点 $D$，求 $\mathit{\Delta BCD}$的面积．

如图，一次函数 $y=\mathit{kx}+b(k\ne 0)$与反比例函数 $y=\frac{m}{x}(m\ne 0,x>0)$图象的两个交点分别为 $A(4,\frac{1}{2})$， $B(1,2)$， $\mathit{AC}\perp x$轴于点 $C$， $\mathit{BD}\perp y$轴于点 $D$．

（1）根据图象直接回答：在第一象限内，当 $x$取何值时，一次函数值大于反比例函数值？

（2）求一次函数的解析式及 $m$的值；

（3） $P$是线段 $\mathit{AB}$上的一点，连接 $\mathit{PC}$， $\mathit{PD}$，若 $\mathit{\Delta PCA}$和 $\mathit{\Delta PDB}$的面积相等，求点 $P$的坐标．

如图已知函数 $y=\frac{k}{x}(k>0,x>0)$的图象与一次函数 $y=\mathit{mx}+5(m<0)$的图象相交不同的点 $A$、 $B$，过点 $A$作 $\mathit{AD}\perp x$轴于点 $D$，连接 $\mathit{AO}$，其中点 $A$的横坐标为 $x_0$， $\mathit{\Delta AOD}$的面积为2．

（1）求 $k$的值及 $x_0=4$时 $m$的值；

（2）记 $\left[\right]$表示为不超过 $x$的最大整数，例如： $[1.4]=1$， $\left[2\right]=2$，设 $t=\mathit{OD}·\mathit{DC}$，若 $-\frac{3}{2}<m<-\frac{5}{4}$，求 $[m^2·t]$值．