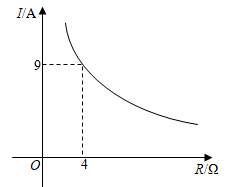
已知蓄电池的电压为定值,使用蓄电池时,电流 (单位: 与电阻 (单位: 是反比例函数关系,它的图象如图所示。下列说法正确的是
| A. |
函数解析式为 |
B. |
蓄电池的电压是 |
| C. |
当 时, |
D. |
当 时, |
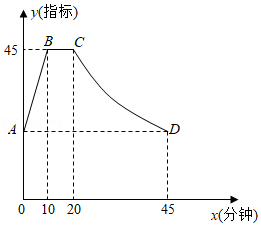
通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标 随时间 (分钟)变化的函数图象如图所示,当 和 时,图象是线段;当 时,图象是反比例函数的一部分.
(1)求点 对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.
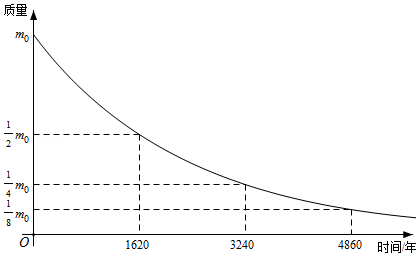
如图为表示镭的放射规律的函数图象,据此可计算 镭缩减为 所用的时间大约是
| A. |
4860年 |
B. |
6480年 |
C. |
8100年 |
D. |
9720年 |
已知蓄电池的电压为定值,使用蓄电池时,电流 (单位: 与电阻 (单位: 是反比例函数关系.当 时, .
(1)写出 关于 的函数解析式;
(2)完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
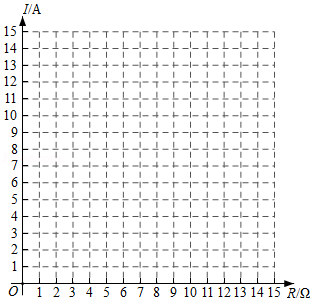
(3)如果以此蓄电池为电源的用电器的限制电流不能超过 ,那么用电器可变电阻应控制在什么范围内?
在 中, 边的长为 , 边上的高为 , 的面积为2.
(1) 关于 的函数关系式是 , 的取值范围是 ;
(2)在平面直角坐标系中画出该函数图象;
(3)将直线 向上平移 个单位长度后与上述函数图象有且只有一个交点,请求出此时 的值.
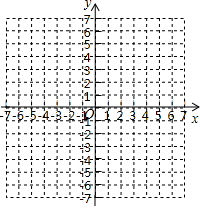
小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间 (单位:秒)与训练次数 (单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
(1)求 与 之间的函数关系式;
(2)当 的值为6,8,10时,对应的函数值分别为 , , ,比较 与 的大小: .
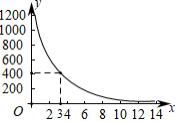
为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要 ;完成2间办公室和1间教室的药物喷洒要 .
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度 (单位: 与时间 (单位: 的函数关系如图所示:校医进行药物喷洒时 与 的函数关系式为 ,药物喷洒完成后 与 成反比例函数关系,两个函数图象的交点为 .当教室空气中的药物浓度不高于 时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.
已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为 (单位:吨 小时),卸完这批货物所需的时间为 (单位:小时).
(1)求 关于 的函数表达式.
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时间为 小时,平均速度为 千米 小时(汽车行驶速度不超过100千米 小时).根据经验, , 的一组对应值如下表:
(千米 小时) |
75 |
80 |
85 |
90 |
95 |
(小时) |
4.00 |
3.75 |
3.53 |
3.33 |
3.16 |
(1)根据表中的数据,求出平均速度 (千米 小时)关于行驶时间 (小时)的函数表达式;
(2)汽车上午 从丽水出发,能否在上午 之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间 满足 ,求平均速度 的取值范围.
在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为 , .
①求 关于 的函数表达式;
②当 时,求 的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?
在四边形 中, , , , 垂直平分 ,点 为垂足.设 , ,则 关于 的函数关系用图象大致可以表示为
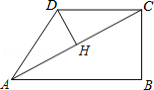
A.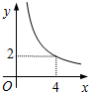 B.
B.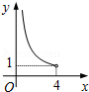
C.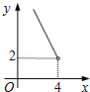 D.
D.
湖州市菱湖镇某养鱼专业户准备挖一个面积为2000平方米的长方形鱼塘.
(1)求鱼塘的长 (米 关于宽 (米 的函数表达式;
(2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米,鱼塘的长为多少米?
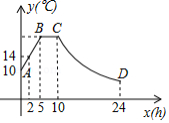
某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度 与时间 之间的函数关系,其中线段 、 表示恒温系统开启阶段,双曲线的一部分 表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度 与时间 的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于 时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
校园超市以4元 件购进某物品,为制定该物品合理的销售价格,对该物品进行试销调查.发现每天调整不同的销售价,其销售总金额为定值,其中某天该物品的售价为6元 件时,销售量为50件.
(1)设售价为 元 件时,销售量为 件.请写出 与 的函数关系式;
(2)若超市考虑学生的消费实际,计划将该物品每天的销售利润定为60元,则该物品的售价应定为多少元 件?
试题篮
()